如图,四棱锥P-ABCD中,AD∥BC,∠ADC= ,
,
PC⊥平面ABCD,点E为AB中点。AC⊥DE,
其中AD=1,PC=2,CD= ;
;
(1)求异面直线DE与PB所成角的余弦值;
(2)求直线PC与平面PDE所成角的余弦值。
如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F.
(1)求证:DE是⊙O的切线.
(2)若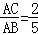 ,求
,求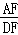 的值.
的值.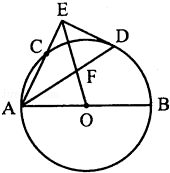
已知函数f(x)=x3+ax2﹣a2x+2,a∈R.
(1)若a<0时,试求函数y=f(x)的单调递减区间;
(2)若a=0,且曲线y=f(x)在点A、B(A、B不重合)处切线的交点位于直线x=2上,证明:A、B 两点的横坐标之和小于4;
(3)如果对于一切x1、x2、x3∈[0,1],总存在以f(x1)、f(x2)、f(x3)为三边长的三角形,试求正实数a的取值范围.
如图,已知椭圆C: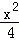 +y2=1的上、下顶点分别为A、B,点P在椭圆上,且异于点A、B,直线AP、BP与直线l:y=﹣2分别交于点M、N,
+y2=1的上、下顶点分别为A、B,点P在椭圆上,且异于点A、B,直线AP、BP与直线l:y=﹣2分别交于点M、N,
(1)设直线AP、BP的斜率分别为k1、k2,求证:k1•k2为定值;
(2)当点P运动时,以MN为直径的圆是否经过定点?请证明你的结论.
如图,在直三棱柱ABC﹣A1B1C1(侧棱和底面垂直的棱柱)中,平面A1BC⊥侧面A1ABB1,AB=BC=AA1=3,线段AC、A1B上分别有一点E、F且满足2AE=EC,2BF=FA1.
(1)求证:AB⊥BC;
(2)求点E到直线A1B的距离;
(3)求二面角F﹣BE﹣C的平面角的余弦值.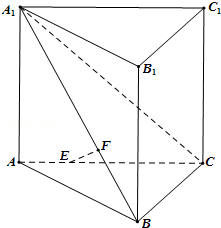
如图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天.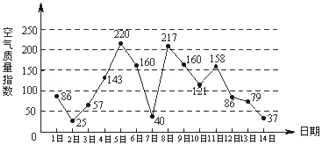
(1)求此人到达当日空气重度污染的概率;
(2)设X是此人停留期间空气质量优良的天数,求X的分布列与数学期望.