选修4 - 4:坐标系与参数方程
已知极坐标系的极点与直角坐标系的原点重合,极轴与 轴的正半轴重合.若曲线
轴的正半轴重合.若曲线 的极坐标方程为
的极坐标方程为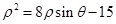 ,曲线
,曲线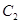 的参数方程为
的参数方程为 (
( 为参数).
为参数).
(1)将 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)若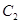 上的点
上的点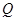 对应的参数为
对应的参数为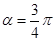 ,
,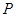 为
为 上的动点,求
上的动点,求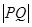 的最小值。
的最小值。
(本小题满分12分)
已知函数 的零点的集合为{0,1},且
的零点的集合为{0,1},且 是f(x)的一个极值点。
是f(x)的一个极值点。
(1)求 的值;
的值;
(2)试讨论过点P(m,0)与曲线y=f(x)相切的直线的条数。
(本小题满分12分)
已知点F( 1,0), 与直线4x+3y + 1 =0相切,动圆M与
与直线4x+3y + 1 =0相切,动圆M与 及y轴都相切. (I )求点M的轨迹C的方程;(II)过点F任作直线l,交曲线C于A,B两点,由点A,B分别向
及y轴都相切. (I )求点M的轨迹C的方程;(II)过点F任作直线l,交曲线C于A,B两点,由点A,B分别向 各引一条切线,切点 分别为P,Q,记
各引一条切线,切点 分别为P,Q,记 .求证
.求证 是定值.
是定值.
(本小题满分12分)
在正四棱锥V - ABCD中,P,Q分别为棱VB,VD的中点, 点M在边BC上,且BM: BC = 1 : 3,AB =2 ,VA =" 6."
,VA =" 6." 
(I )求证CQ∥平面PAN;
(II)求证:CQ⊥AP.
(本小题满分12分)
PM2. 5是指大气中直径小于或等于2. 5微米的颗粒物,也称为 可人肺颗粒物.我国PM2. 5标准采用世卫组织设定的最宽限 值,即PM2.5日均值在35微克/立方米以下空气质量为一级; 在35微克/立方米~75微克/立方米之间空气质量为二级;在 75微克/立方米以上空气质量为超标.
某市环保局从市区2012年全年每天的PM2.5监测数据中 随机抽取15天的数据作为样本,监测值如茎叶图所示(十位为 茎,个位为叶)
(I)从这9天的数据中任取2天的数据,求恰有一天空气质量达到一级的概率;
(II) 以这9天的PM2. 5日均值来估计供暖期间的空气质量情况,则供暖期间(按150天计算)中大约有多少天的空气质量达到一级.
(本小题满分12分)
已知数列{an}、{bn}分别是首项均为2的各项均为正数的等比数列和等差数列,且
(I)求数列{an}、{bn}的通项公式;
(II )求使 <0.001成立的最小的n值.
<0.001成立的最小的n值.