某企业在第
年初购买一台价值为
万元的设备
的价值在使用过程中逐年减少,从第
年到第
年,每年初
的价值比上年初减少
万元;从第
年开始,每年初
的价值为上年初的
.
(1)求第
年初
的价值
的表达式;
(2)设
,若
大于80万元,则
继续使用,否则须在第
年初对
更新,证明:须在第9年初对
更新.
【2015高考新课标2,理24】(本小题满分10分)选修4-5不等式选讲
设 均为正数,且
均为正数,且 ,证明:
,证明:
(Ⅰ)若 ,则
,则 ;
;
(Ⅱ) 是
是 的充要条件.
的充要条件.
【2015高考新课标2,理23】选修4-4:坐标系与参数方程
在直角坐标系 中,曲线
中,曲线 (
( 为参数,
为参数, ),其中
),其中 ,在以
,在以 为极点,
为极点, 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线 ,曲线
,曲线 .
.
(Ⅰ)求 与
与 交点的直角坐标;
交点的直角坐标;
(Ⅱ)若 与
与 相交于点
相交于点 ,
, 与
与 相交于点
相交于点 ,求
,求 的最大值.
的最大值.
【2015高考新课标2,理22】选修4—1:几何证明选讲
如图, 为等腰三角形
为等腰三角形 内一点,圆
内一点,圆 与
与 的底边
的底边 交于
交于 、
、 两点与底边上的高
两点与底边上的高 交于点
交于点 ,与
,与 、
、 分别相切于
分别相切于 、
、 两点.
两点.
(Ⅰ)证明: ;
;
(Ⅱ)若 等于
等于 的半径,且
的半径,且 ,求四边形
,求四边形 的面积.
的面积.
【2015高考上海,理19】如图,在长方体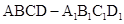 中,
中,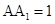 ,
,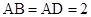 ,
,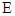 、
、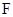 分别是
分别是 、
、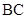 的中点.证明
的中点.证明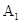 、
、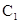 、
、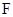 、
、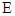 四点共面,并求直线
四点共面,并求直线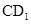 与平面
与平面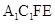 所成的角的大小.
所成的角的大小.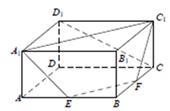
【2015高考湖南,理19】如图,已知四棱台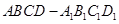 上、下底面分别是边长为3和6的正方形,
上、下底面分别是边长为3和6的正方形,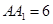 ,且
,且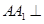 底面
底面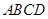 ,点
,点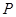 ,
,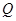 分别在棱
分别在棱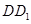 ,BC上.
,BC上.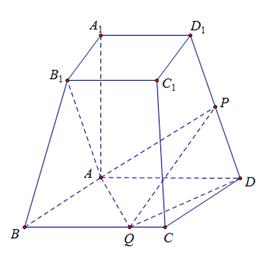
(1)若P是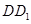 的中点,证明:
的中点,证明: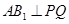 ;
;
(2)若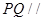 平面
平面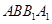 ,二面角
,二面角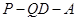 的余弦值为
的余弦值为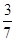 ,求四面体
,求四面体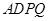 的体积.
的体积.