某 企
企 业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的体积为
业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的体积为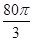 立方米,且
立方米,且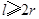 .假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为
.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为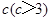 .设该容器的建造费用为
.设该容器的建造费用为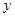 千元.
千元.
(Ⅰ)写出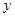
 关于
关于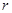 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域;
(Ⅱ)求该容器的建造费用最小时的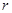 .
.
(本小题满分12分)在△ABC中,a,b,c分别是A,B,C的对边,且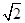 sin A=
sin A=
(1)若a2-c2=b2-mbc,求实数m的值;
(2)若a=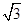 ,求△ABC面积的最大值.
,求△ABC面积的最大值.
(本小题满分12分)已知等比数列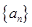 满足
满足 ,数列
,数列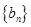 满足
满足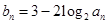 .
.
(Ⅰ)求数列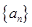 和
和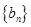 的通项公式;
的通项公式;
(Ⅱ)令 ,求数列
,求数列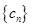 的前n项和
的前n项和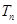 ;
;
(Ⅲ)若 ,求对所有的正整数n都有
,求对所有的正整数n都有 成立的
成立的 的范围.
的范围.
(本小题满分12分)如图,在四棱锥P﹣ABCD中,底面ABCD是梯形,PA⊥底面ABCD,其中BA⊥AD,AD∥BC, AC与BD交于点O,M是AB边上的点,且 ,已知PA=AD=4,AB=3,BC=2.
,已知PA=AD=4,AB=3,BC=2.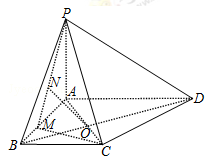
(Ⅰ)求平面PAD与平面PMC所成锐二面角的正切值;
(Ⅱ)已知N是PM上一点,且ON∥平面PCD,求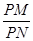 的值.
的值.
(本小题满分12分)已知数列 的前n项和为
的前n项和为 ,首项
,首项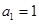 ,且对于任意
,且对于任意 ,都有
,都有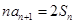
(Ⅰ)求 的通项公式;
的通项公式;
(Ⅱ)设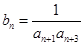 ,且数列的前n项之和为
,且数列的前n项之和为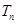 ,求证:
,求证: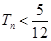
在如图所示的多面体ABCDE中,AB∥DE,AB⊥AD,△ACD是正三角形,AD=DE=2AB=2, ,F是CD的中点.
,F是CD的中点.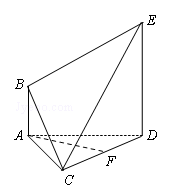
(Ⅰ)求证AF∥平面BCE;
(Ⅱ)求多面体ABCDE的体积.