(本小题满分12分)盒子里装有6件包装完全相同的产品,已知其中有2件次品,其余4件是合格品。为了找到2件次品,只好将盒子里的这些产品包装随机打开检查,直到两件次品被全部检查或推断出来为止。记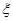 表示将两件次品被全部检查或推断出来所需检查次数。
表示将两件次品被全部检查或推断出来所需检查次数。
(I)求两件次品被全部检查或推断出来所需检查次数恰为4次的概率;
(II)求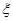 的分布列和数学期望。
的分布列和数学期望。
【改编】(本小题满分12分)函数 部分图象如图所示.
部分图象如图所示.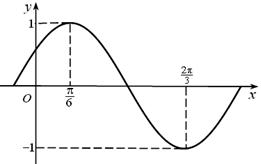
(Ⅰ)求 的最小正周期及解析式;
的最小正周期及解析式;
(Ⅱ)设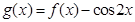 ,求函数
,求函数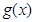 在区间
在区间 上的单调性.
上的单调性.
设函数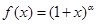 的定义域是
的定义域是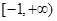 ,其中常数
,其中常数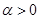 .
.
(1)若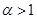 ,求
,求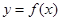 的过原点的切线方程.
的过原点的切线方程.
(2)当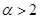 时,求最大实数
时,求最大实数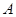 ,使不等式
,使不等式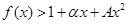 对
对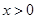 恒成立.
恒成立.
(3)证明当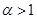 时,对任何
时,对任何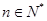 ,有
,有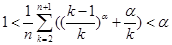 .
.
(本小题满分13分)已知椭圆C: (a>b>0)的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
(a>b>0)的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
(1)求椭圆C的标准方程.
(2)设F为椭圆C的左焦点,T为直线x=-3上任意一点,过F作TF的垂线交椭圆C于点P,Q.
①证明:OT平分线段PQ(其中O为坐标原点);
②当 最小时,求点T的坐标.
最小时,求点T的坐标.
(本小题满分12分)已知 是等差数列
是等差数列 的前n项和,数列
的前n项和,数列 是等比数列,
是等比数列, 恰为
恰为 的等比中项,圆
的等比中项,圆 ,直线
,直线 ,对任意
,对任意 ,直线
,直线 都与圆C相切.
都与圆C相切.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若 时,
时, 的前n项和为
的前n项和为 ,求证:对任意
,求证:对任意 ,都有
,都有
(本小题满分12分)如图,四边形 是正方形,△
是正方形,△ 与△
与△ 均是以
均是以 为直角顶点的等腰直角三角形,点
为直角顶点的等腰直角三角形,点 是
是 的中点,点
的中点,点 是边
是边 上的任意一点.
上的任意一点.
(1)求证: ;
;
(2)求二面角 的平面角的正弦值.
的平面角的正弦值.