已知 的解为条件
的解为条件 ,关于
,关于 的不等式
的不等式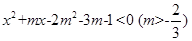 的解为条件
的解为条件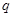 .
.
(Ⅰ)若 是
是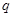 的充分不必要条件时,求实数
的充分不必要条件时,求实数 的取值范围.
的取值范围.
(Ⅱ)若 是
是 的充分不必要条件时,求实数
的充分不必要条件时,求实数 的取值范围.
的取值范围.
已知等差数列 的公差为
的公差为 ,且
,且 ,
, ,
, 成等比数列.
成等比数列.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设数列 的前
的前 学科王项和为
学科王项和为 ,求证:
,求证: .
.
某家居装饰设计的形状是如图所示的直三棱柱 ,其中,
,其中, ,
, 是边长为2(单位:米)的正方形,
是边长为2(单位:米)的正方形, ,点
,点 为棱
为棱 上的动点.
上的动点.
(Ⅰ)现需要对该装饰品的表面进行涂漆处理,假设每平方米的油漆费是40元,则需油漆费多少元?(提示: ,结果保留到整数位)
,结果保留到整数位)
(Ⅱ)当点 为何位置时,
为何位置时, 平面
平面 ?
?
某小区内有如图所示的一矩形花坛,现将这一矩形花坛 扩建成一个更大的矩形花坛
扩建成一个更大的矩形花坛 ,要求
,要求 点在
点在 上,
上, 点在
点在 上,且对角线
上,且对角线 过
过 点,已知
点,已知 米,
米, 米.
米.
(Ⅰ)要使矩形 的面积大于32平方米,则
的面积大于32平方米,则 的长应在什么范围内?
的长应在什么范围内?
(Ⅱ)当 的长度是多少时,矩形花坛
的长度是多少时,矩形花坛 的面积最小?并求出最小值.
的面积最小?并求出最小值.
已知直线 与圆
与圆 相交于不同两点
相交于不同两点 ,
, .
.
(Ⅰ)求实数 的取值范围
的取值范围
(Ⅱ)是否存在实数 ,使得过点
,使得过点 的直线
的直线 垂直平分弦
垂直平分弦 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
在 中,角
中,角 、
、 、
、 对的边分别为
对的边分别为 、
、 、
、 ,且
,且
(Ⅰ)求 的值;
的值;
(Ⅱ)若 ,求
,求 的面积
的面积 .
.