(本小题满分14分)
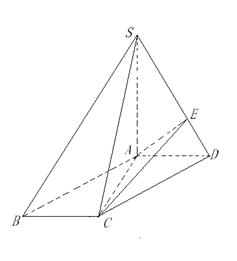
如图,在四棱锥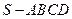 中,底面
中,底面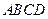 为平行四边形,
为平行四边形,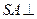 平面
平面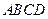 ,
,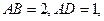
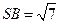
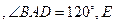 在棱
在棱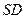 上
上 .
.
(Ⅰ)当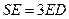 时,求证
时,求证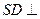 平面
平面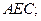
(Ⅱ)当二面角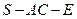 的大小为
的大小为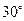 时,求直线
时,求直线 与平面
与平面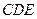 所成角的正弦值.
所成角的正弦值.
.(本小题满分12分).
如图,已知某椭圆的焦点是F1(-4,0)、F2(4,0),过点F2并垂直于x轴的直线与椭圆的一个交点为B,且|F1B|+|F2B|=10,椭圆上不同的两点A(x1,y1),C(x2,y2)满足条件:|F2A|、|F2B|、|F2C|成等差数列.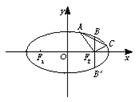
(1)求该弦椭圆的方程;
(2)求弦AC中点的横坐标;
(3)设弦AC的垂直平分线的方程为y=kx+m,求m的取值范围.
(本小题满分12分)
已知双曲线的中心在原点,对称轴为坐标轴,焦点在x轴上,两准线间的距离为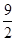 ,并且与直线
,并且与直线 相交所得线段中点的横坐标为
相交所得线段中点的横坐标为 ,求这个双曲线方程。
,求这个双曲线方程。
(本小题满分12分)
如图,在直四棱柱ABCD-A B
B C
C D
D 中,底面ABCD为等腰梯形,AB//CD,AB="4," BC="CD=2," AA
中,底面ABCD为等腰梯形,AB//CD,AB="4," BC="CD=2," AA ="2," E、E
="2," E、E 、F分别是棱AD、AA
、F分别是棱AD、AA 、AB的中点。
、AB的中点。
(1)证明:直线EE
 //平面FCC
//平面FCC ;
;
(2)求二面角B-FC -C的余弦值。
-C的余弦值。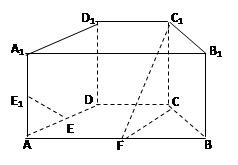
(本小题满分12分)如图四棱锥 的底面是正方形,
的底面是正方形,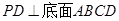 ,点E在棱PB上,O为AC与BD的交点。
,点E在棱PB上,O为AC与BD的交点。
(1)求证:平面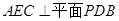 ;
;
( 2)当E为PB中点时,求证:
2)当E为PB中点时,求证: //平面PDA,
//平面PDA, //平面PDC。
//平面PDC。
(3)当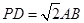 且E为PB的中点时,求
且E为PB的中点时,求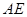 与平面
与平面 所成的角的大小。
所成的角的大小。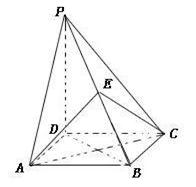
(本小题满分12分)设 ,其中
,其中 为正实数
为正实数
(1)当
 时,求
时,求 的极值点;
的极值点;
(2)若 为
为 上的单调函数,求
上的单调函数,求 的取值范围。
的取值范围。