已知二次函数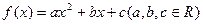 对任意实数
对任意实数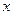 ,都有
,都有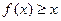 ,且
,且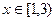 时,有
时,有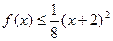 成立,(1)证明f(2)=2;(2)若
成立,(1)证明f(2)=2;(2)若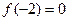 ,求f(x)的表达式;
,求f(x)的表达式; ⑶ 在题(2)的条件下设
⑶ 在题(2)的条件下设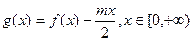 ,若
,若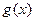 图象上的点都位于直线
图象上的点都位于直线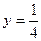 的上方,求实数m的取值范围.
的上方,求实数m的取值范围.
围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用的旧墙需维修),其他三面围墙要新建,在旧墙对面的新墙上要留一个宽度为2m的进出口,如图所示已知旧墙的维修 费用为45元/m,新墙的造价为180元/m,设利用的旧墙长
费用为45元/m,新墙的造价为180元/m,设利用的旧墙长 度为x(单位:m),修建此矩形场地围墙的总费用为y(单位:元)
度为x(单位:m),修建此矩形场地围墙的总费用为y(单位:元)
⑴将y表示为x的函数;
⑵写出f(x)的单调区间(不必证明)
⑶根据⑵,试确定x, 使修建此矩形场地围墙的总费用最小,并求出最小总费用。
使修建此矩形场地围墙的总费用最小,并求出最小总费用。
已知函数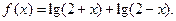
(1) 求函数
求函数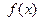 的定义域;
的定义域;
(2)记函数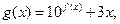 求
求 函数
函数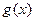 的值域;
的值域;
(3)若不等式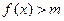 有解,求实数
有解,求实数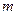 的取值范围.
的取值范围.
本题满分14分)已知z是复数,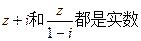 ,⑴求复数z;⑵设关于
,⑴求复数z;⑵设关于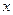 的方程
的方程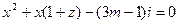 有实根,求纯虚数
有实根,求纯虚数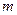
已知函数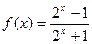 ,(1)判断
,(1)判断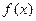 的奇偶性;(2)判断并用定义证明
的奇偶性;(2)判断并用定义证明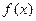 在
在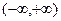 上的单调性
上的单调性