已知数列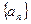 的首项为
的首项为 =3,通项
=3,通项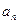 与前n项和
与前n项和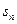 之间满足2
之间满足2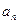 =
=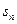 ·
·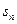
(n≥2)。
(1)求证: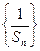 是等差数列,并求公差;
是等差数列,并求公差;
(2)求数列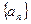 的通项公式。
的通项公式。
在 中,
中,  所对边分别为
所对边分别为 .
.
已知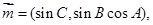
 ,且
,且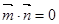 .
.
(Ⅰ)求 大小;(Ⅱ)若
大小;(Ⅱ)若 求
求 的面积S的大小.
的面积S的大小.
已知集合 的元素全为实数,且满足:若
的元素全为实数,且满足:若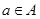 ,则
,则 。
。
(1)若 ,求出
,求出 中其它所有元素;
中其它所有元素;
(2)0是不是集合 中的元素?请你设计一个实数
中的元素?请你设计一个实数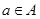 ,再求出
,再求出 中的所有元素?
中的所有元素?
(3)根据(1)(2),你能得出什么结论。
设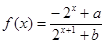 (
( 为实常数).
为实常数).
(1)当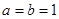 时,证明:
时,证明: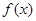 不是奇函数;
不是奇函数;
(2)设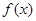 是奇函数,求
是奇函数,求 与
与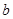 的值;
的值;
(3)在满足(2)且当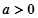 时,若对任意的
时,若对任意的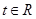 ,不等式
,不等式
恒成立,求 的取值范围.
的取值范围.
某光线通过一块玻璃,其强度要损失 ,把几块这样的玻璃重叠起来,设光线原来的强度为
,把几块这样的玻璃重叠起来,设光线原来的强度为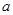 ,通过
,通过 块玻璃后强度为
块玻璃后强度为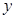 .
.
(1)写出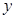 关于
关于 的函数关系式;
的函数关系式;
(2)通过多少块玻璃后,光线强度减弱到原来的 以下?(
以下?( 
设函数 ,
, ,
,
(1)若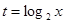 ,求
,求 取值范围;
取值范围;
(2)求 的最值,并给出最值时对应的x的值。
的最值,并给出最值时对应的x的值。