已知抛物线y1=x2+4x+1的图象向上平移m个单位(m>0)得到的新抛物线过点(1,8).
(1)求m的值,并将平移后的抛物线解析式写成y2=a(x﹣h)2+k的形式;
(2)将平移后的抛物线在x轴下方的部分沿x轴翻折到x轴上方,与平移后的抛物线没有变化的部分构成一个新的图象.请写出这个图象对应的函数y的解析式,并在所给的平面直角坐标系中直接画出简图,同时写出该函数在﹣3<x≤ 时对应的函数值y的取值范围;
时对应的函数值y的取值范围;
(3)设一次函数y3=nx+3(n≠0 ),问是否存在正整数n使得(2)中函数的函数值y=y3时,对应的x的值为﹣1<x<0,若存在,求出n的值;若不存在,说明理由.
),问是否存在正整数n使得(2)中函数的函数值y=y3时,对应的x的值为﹣1<x<0,若存在,求出n的值;若不存在,说明理由.
如图,定义:若双曲线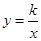
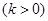 与它的其中一条对称轴y=x相交于A、B两点,则线段AB称为双曲线
与它的其中一条对称轴y=x相交于A、B两点,则线段AB称为双曲线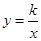
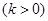 的对径.
的对径.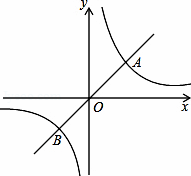
(1)求双曲线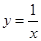 的对径的长;
的对径的长;
(2)若双曲线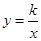
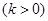 的对径的长是10
的对径的长是10 ,求k的值;
,求k的值;
(3)仿照上述定义,定义双曲线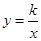
 的对径.
的对径.
如图,在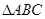 中,
中, ,点
,点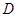 在
在 的延长线上,且
的延长线上,且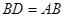 ,过
,过 作BE
作BE AC,与
AC,与 的垂线
的垂线 交于点
交于点 ,
,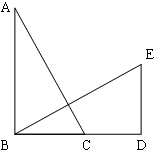
(1)求证: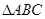 ≌
≌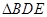 .
.
(2)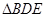 可由
可由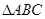 旋转得到,请用直尺和圆规作出旋转中心
旋转得到,请用直尺和圆规作出旋转中心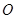 (保留作图痕迹,不写作法).
(保留作图痕迹,不写作法).
(1)计算: ;
;
(2)解方程组:
把两块全等的直角三角形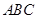 和
和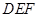 叠放在一起,使三角板
叠放在一起,使三角板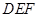 的锐角顶点
的锐角顶点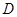 与三角板
与三角板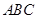 的斜边中点
的斜边中点 重合,其中
重合,其中 ,
, ,
, ,把三角板
,把三角板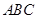 固定不动,让三角板
固定不动,让三角板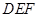 绕点
绕点 旋转,设射线
旋转,设射线 与射线
与射线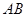 相交于点
相交于点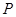 ,射线
,射线 与线段
与线段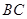 相交于点
相交于点 .
.
(1)如图1,当射线 经过点
经过点 ,即点
,即点 与点
与点 重合时,易证
重合时,易证 .此时,
.此时,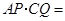 ;将三角板
;将三角板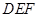 由图1所示的位置绕点
由图1所示的位置绕点 沿逆时针方向旋转,设旋转角为
沿逆时针方向旋转,设旋转角为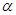 .其中
.其中 ,问
,问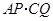 的值是否改变?答: (填“会”或“不会”);若改变,
的值是否改变?答: (填“会”或“不会”);若改变,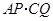 的值为 (不必说明理由);
的值为 (不必说明理由);
(2)在(1)的条件下,设 ,两块三角板重叠面积为
,两块三角板重叠面积为 ,求
,求 与
与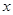 的函数关系式.(图2,图3供解题用)
的函数关系式.(图2,图3供解题用)
某瓜果基地市场部为指导该基地某种蔬菜的生产和销售,对往年的市场行情和生产情况进行了调查,提供了如下两个信息图,如甲、乙两图。
注:甲、乙两图中的A、B、C、D、E、F、G、H所对应的纵坐标分别指相应月份每千克该种蔬菜的售价和成本(生产成本6月份最低,甲图的图象是线段,乙图的图象是抛物线的一部分)。请你根据图象提供的信息说明:
(1)在3月份出售这种蔬菜,每千克的收益是多少元?(收益=售价-成本)
(2)哪个月出售这种蔬菜,每千克的收益最大?最大收益是多少?说明理由。