如图l0．在平面直角坐标系xoy中，AB在x轴上，AB=10．以AB为直径的⊙O’与y轴正半轴交于点C．连接BC，AC。CD是⊙O’的切线．AD⊥CD于点D，tan∠CAD=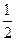
，抛物线
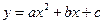过A、B、C三点。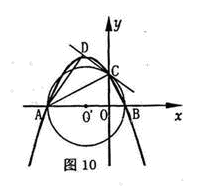
（1）求证：∠CAD=∠CAB；
（2）①求抛物线的解析式；
②判断抛物线的顶点E是否在直线CD上．并说明理由：
（3）在抛物线上是否存在一点P，使四边形PBCA是直角梯形．若存在，直接写出点P的坐标(不写求解过程)；若不存在．请说明理由．
（1）计算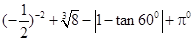
（2）解不等式组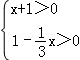
并把解集在数轴上表示出来．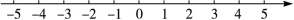
如图，抛物线y=－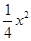
+
+4的图象与y轴交于点A，与x轴交于B、C两点，其对称轴与x轴交于点D，连接AC．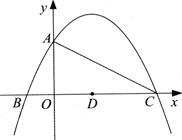
（1）点A的坐标为_______ ，点C的坐标为_______ ；
（2）线段AC上是否存在点E，使得△EDC为等腰三角形?若存在，求出所有符合条件的点E的坐标；若不存在，请说明理由；
（3）点P为x轴上方的抛物线上的一个动点，连接PA、PC，若所得△PAC的面积为S，则S取何值时，相应的点P有且只有2个?
从无锡供电公司获悉，现我市执行阶梯电价。居民月用电量分为三个档次，第一档230度及以内，维持现行电价标准即每度按0．53元收取；第二档为231度至400度，即每个月用电量超出230度不超过400度部分，按照每度0．58元收取；第三档为高于400度部分。，即超出400度部分，按照每度0．83元收取
请完成下列问题：
（1）如果该地区某户居民2014年8月用电310度，则该居民8月应付电费为元．
（2）实行阶梯电价后，如果月用电量用x（度）表示，月支出电费用y（元）表示，小红、小明、小丽三人绘制了如下大致图像，你认为正确的是．
（3）小明同学家2014年11、12两月共用电460度，且11月份用电量少于12月份，他通过计算发现：他这两个月的电费比调整前多出了2．5元。你能求出他家11、12两月用电量分别是多少吗？
如图①所示，已知A、B为直线a上两点，点C为直线a上方一动点，连接AC、BC，分别以AC、BC为边向△ABC外作正方形CADF和正方形CBEG，过点D作D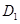
⊥a于点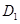，过点E作E
⊥a于点。
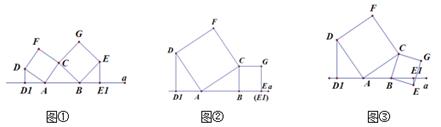
（1）如图②，当点E恰好在直线a上时，（此时E1和E重合）。试说明D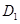=AB；
（2）如图①中，当D、E两点都在直线a的上方时，试探求三条线段D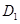、E、AB之间的数量关系，并说明理由。
（3）如图③，当点E在直线a的下方时，请直接写出三条线段D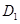、E、AB之间的数量关系。（不需要证明）
如图，⊙O的直径AC与弦BD相交于点F，点E是DB延长线上一点，∠EAB=∠ADB．
（1）求证：EA是⊙O的切线；
（2）已知点B是EF的中点，求证：以A、B、C为顶点的三角形与△AEF相似；
（3）已知AF=4，CF=2，在（2）的条件下，求AE的长．