设函数 定义在
定义在 上,
上,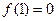 ,导函数
,导函数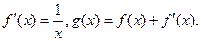
(Ⅰ)求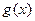 的单调区间和最小值;
的单调区间和最小值;
(Ⅱ)求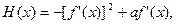 在
在 上的最大值。
上的最大值。
某校教务处要对高三上学期期中数学试卷进行调研,考察试卷中某道填空题的得分情况.已知该题有两空,第一空答对得3分,答错或不答得0分;第二空答对得2分,答错或不答得0分.第一空答对与否与第二空答对与否是相互独立的.从该校1468份试卷中随机抽取1000份试卷,其中该题的得分组成容量为1000的样本,统计结果如下表:
| 第一空得分情况 |
第二空得分情况 |
|||||
| 得分 |
0 |
3 |
得分 |
0 |
2 |
|
| 人数 |
198 |
802 |
人数 |
698 |
302 |
(Ⅰ)求样本试卷中该题的平均分,并据此估计该校高三学生该题的平均分.
(Ⅱ)该校的一名高三学生因故未参加考试,如果这名学生参加考试,以样本中各种得分情况的频率(精确到0.1)作为该同学相应的各种得分情况的概率.试求该同学这道题得分 的数学期望.
的数学期望.
已知函数 ,且定义域为(0,2).
,且定义域为(0,2).
(1)求关于x的方程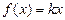 +3在(0,2)上的解;
+3在(0,2)上的解;
(2)若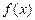 是定义域(0,2)上的单调函数,求实数
是定义域(0,2)上的单调函数,求实数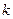 的取值范围;
的取值范围;
(3)若关于x的方程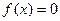 在(0,2)上有两个不同的解
在(0,2)上有两个不同的解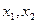 ,求k的取值范围。
,求k的取值范围。
已知圆C: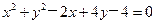 ,直线
,直线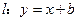 .
.
(1)若直线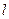 与圆C相切,求实数b的值;
与圆C相切,求实数b的值;
(2)是否存在直线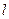 ,使
,使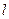 与圆C交于A、B两点,且以AB为直径的圆过原点.如果存在,求出直线
与圆C交于A、B两点,且以AB为直径的圆过原点.如果存在,求出直线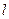 的方程,如果不存在,请说明理由.
的方程,如果不存在,请说明理由.
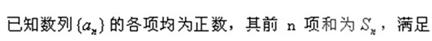

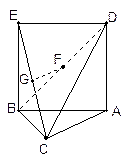
如图,三角形ABC中,AC=BC= ,ABED是边长为1的正方形,平面ABED⊥底面ABC,若G、F分别是EC、BD的中点.
,ABED是边长为1的正方形,平面ABED⊥底面ABC,若G、F分别是EC、BD的中点.
(1)求证:GF//底面ABC;
(2)求证:AC⊥平面EBC;
(3)求几何体ADEBC的体积V.