已知二次函数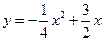 的图象如图.
的图象如图.
(1)求它的对称轴与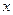 轴交点D的坐标;
轴交点D的坐标;
(2)将该抛物线沿它的对称轴向上平移,设平移后的抛物线与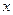 轴,
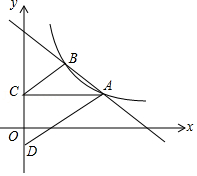
轴,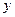 轴的交点分别为A、B、C三点,若∠ACB=90°,求此时抛物线的解析式;
轴的交点分别为A、B、C三点,若∠ACB=90°,求此时抛物线的解析式;
(3)设(2)中平移后的抛物线的顶点为M,以AB为直径,D为圆心作⊙D,试判断直线CM与⊙D的位置关系,并说明理由.
如图,在平面直角坐标系中,直线 与函数 的图象交于点 , .过点 作 平行于 轴交 轴于点 ,在 轴负半轴上取一点 ,使 ,且 的面积是6,连接 .
(1)求 , , 的值;
(2)求 的面积.
如图,一枚运载火箭从距雷达站 处 的地面 处发射,当火箭到达点 , 时,在雷达站 处测得点 , 的仰角分别为 , ,其中点 , , 在同一条直线上.求 , 两点间的距离(结果精确到 .
(参考数据: , , .

图①、图②、图③都是由边长为1的小等边三角形构成的网格,每个小等边三角形的顶点称为格点.线段 的端点在格点上.

(1)在图①、图2中,以 为边各画一个等腰三角形,且第三个顶点在格点上;(所画图形不全等)
(2)在图③中,以 为边画一个平行四边形,且另外两个顶点在格点上.
某商场甲、乙、丙三名业务员5个月的销售额(单位:万元)如下表:
|
月份 销售额 人员 |
第1月 |
第2月 |
第3月 |
第4月 |
第5月 |
|
甲 |
7.2 |
9.6 |
9.6 |
7.8 |
9.3 |
|
乙 |
5.8 |
9.7 |
9.8 |
5.8 |
9.9 |
|
丙 |
4 |
6.2 |
8.5 |
9.9 |
9.9 |
(1)根据上表中的数据,将下表补充完整:
|
统计值 数值 人员 |
平均数(万元) |
中位数(万元) |
众数(万元) |
|
甲 |
8.7 |
9.3 |
9.6 |
|
乙 |
8.2 |
|
5.8 |
|
丙 |
7.7 |
8.5 |
|
(2)甲、乙、丙三名业务员都说自己的销售业绩好,你赞同谁的说法?请说明理由.
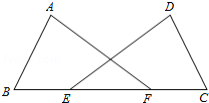
如图,点 、 在 上, , , .求证: .