(本小题满分12分)
袋中有4个黑球、3个白球、2个红球,从中任取2个球,每取到一个黑球记0分,每取到一个白球记1分,每取到一个红球记2分,用X表示得分数.
(1)求X的概率分布列;
(2)求X的数学期望EX.
如图,在多面体 中,四边形
中,四边形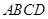 是菱形,
是菱形, 相交于点
相交于点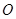 ,
,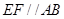 ,
,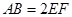 ,平面
,平面
 平面
平面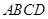 ,
, ,点
,点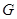 为
为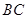 的中点.
的中点.
(1)求证:直线 平面
平面 ;
;
(2)求证:直线
 平面
平面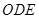 .
.
在平面直角坐标系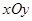 中,角
中,角 的终边经过点
的终边经过点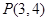 .
.
(1)求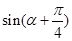 的值;
的值;
(2)若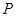 关于
关于 轴的对称点为
轴的对称点为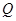 ,求
,求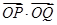 的值.
的值.
已知数列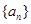 中
中
 .
.
(1)是否存在实数 ,使数列
,使数列 是等比数列?若存在,求
是等比数列?若存在,求 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(2)若 是数列
是数列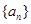 的前
的前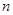 项和,求满足
项和,求满足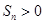 的所有正整数
的所有正整数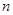 .
.
已知函数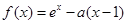 ,其中
,其中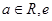 为自然对数底数.
为自然对数底数.
(1)当 时,求函数
时,求函数 在点
在点 处的切线方程;
处的切线方程;
(2)讨论函数 的单调性,并写出相应的单调区间;
的单调性,并写出相应的单调区间;
(3)已知 ,若函数
,若函数 对任意
对任意 都成立,求
都成立,求 的最大值.
的最大值.
如图,已知椭圆 ,点B是其下顶点,过点B的直线交椭圆C于另一点A(A点在
,点B是其下顶点,过点B的直线交椭圆C于另一点A(A点在 轴下方),且线段AB的中点E在直线
轴下方),且线段AB的中点E在直线 上.
上.
(1)求直线AB的方程;
(2)若点P为椭圆C上异于A、B的动点,且直线AP,BP分别交直线 于点M、N,证明:OM·ON为定值.
于点M、N,证明:OM·ON为定值.