(本小题满分12分)
设函数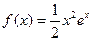 .
.
⑴求函数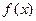 的单调区间;
的单调区间;
⑵若当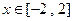 时,不等式
时,不等式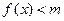 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
求值:(1)
(2)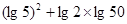
已知集合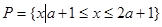 ,集合
,集合
(1)若 ,求集合
,求集合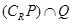 ;(2)若
;(2)若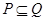 ,求实数
,求实数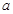 的取值范围
的取值范围
已知函数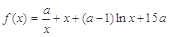 ,
, ,其中
,其中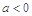 且
且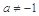 .
.
(Ⅰ) 当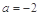 ,求函数
,求函数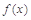 的单调递增区间;
的单调递增区间;
(Ⅱ)若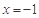 时,函数
时,函数 有极值,求函数
有极值,求函数 图象的对称中心的坐标;
图象的对称中心的坐标;
(Ⅲ)设函数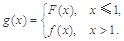 (
(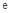 是自然对数的底数),是否存在a使
是自然对数的底数),是否存在a使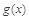 在
在 上为减函数,若存在,求实数a的范围;若不存在,请说明理由.
上为减函数,若存在,求实数a的范围;若不存在,请说明理由.
某地区注重生态环境建设,每年用于改造生态环境总费用为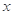 亿元,其中用于风景区改造为
亿元,其中用于风景区改造为 亿元。该市决定建立生态环境改造投资方案,该方案要求同时具备下列三个条件:①每年用于风景区改造费用
亿元。该市决定建立生态环境改造投资方案,该方案要求同时具备下列三个条件:①每年用于风景区改造费用 随每年改造生态环境总费用
随每年改造生态环境总费用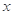 增加而增加;②每年改造生态环境总费用至少
增加而增加;②每年改造生态环境总费用至少 亿元,至多
亿元,至多 亿元;③每年用于风景区改造费用
亿元;③每年用于风景区改造费用 不得低于每年改造生态环境总费用
不得低于每年改造生态环境总费用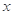 的15%,但不得高于每年改造生态环境总费用
的15%,但不得高于每年改造生态环境总费用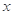 的25%.
的25%.
若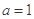 ,
,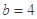 ,请你分析能否采用函数模型y=
,请你分析能否采用函数模型y=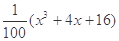 作为生态环境改造投资方案.
作为生态环境改造投资方案.
在平面直角坐标系 中,已知圆
中,已知圆 :
: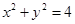 和直线
和直线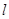 :
: ,
, 为
为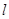 上一动点,
上一动点, ,
,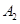 为圆
为圆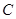 与
与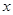 轴的两个交点,直线
轴的两个交点,直线 ,
, 与圆
与圆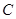 的另一个交点分别为
的另一个交点分别为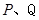 .
.
(1)若 点的坐标为(4,2),求直线
点的坐标为(4,2),求直线 方程;
方程;
(2)求证直线 过定点,并求出此定点的坐标.
过定点,并求出此定点的坐标.