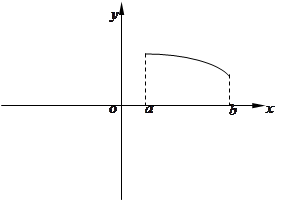(本小题满分12分)
设函数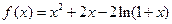 .
.
(1)求函数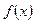 的单调区间;
的单调区间;
(2)当 时,是否存在整数
时,是否存在整数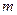 ,使不等式
,使不等式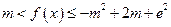 恒成立?若
恒成立?若
存在,求整数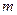 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
(3)关于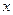 的方程
的方程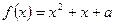 在
在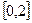 上恰有两个相异实根,求实数
上恰有两个相异实根,求实数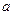 的取值范围。
的取值范围。
设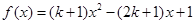 ,
,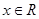 .
.
(1)若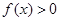 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(2)若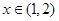 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)当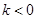 时,解不等式
时,解不等式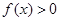 .
.
已知集合M={1,2,3,4,5}, .
.
(1)用列举法表示集合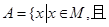
 ;
;
(2)设N是M的非空真子集,且 时,有
时,有 ,试写出所有集合N;
,试写出所有集合N;
(3)已知M的非空子集个数为31个,依次记为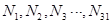 ,分别求出它们各自的元素之和,结果依次记为
,分别求出它们各自的元素之和,结果依次记为 ,试计算:
,试计算: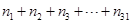 的值.
的值.
已知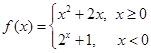 .
.
(1)已知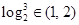 ,分别求
,分别求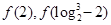 的值;
的值;
(2)画出函数 的图像,并指出函数的单调区间(不要求证明);
的图像,并指出函数的单调区间(不要求证明);
(3)解不等式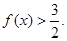

将52名志愿者分成A,B两组参加义务植树活动,A组种植150捆白杨树苗,B组种植200捆沙棘树苗. 假定A,B两组同时开始植树.
(1)根据历年统计,每名志愿者种植一捆白杨树苗用时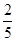 小时,种植一捆沙棘用时
小时,种植一捆沙棘用时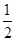 小时,应如何分配A,B两组的人数,使植树活动持续的时间最短?
小时,应如何分配A,B两组的人数,使植树活动持续的时间最短?
(2)在按(1)分配的人数种植1小时后发现,每名志愿者种植一捆白杨仍用时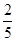 小时,而每名志愿者种植一捆沙棘实际用时
小时,而每名志愿者种植一捆沙棘实际用时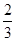 小时,于是,从A组抽调6名志愿者加入B组继续种植,求植树活动持续的时间.
小时,于是,从A组抽调6名志愿者加入B组继续种植,求植树活动持续的时间.
已知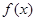 在定义域上是奇函数,且在
在定义域上是奇函数,且在 上是减函数,图像如图所示.
上是减函数,图像如图所示.
(1)化简: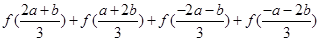 ;
;
(2)画出函数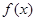 在
在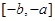 上的图像;
上的图像;
(3)证明: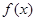 在
在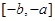 上是减函数.
上是减函数.