（本小题满分12分）
某农场计划种植某种新作物，为此对这种作物的两个品种（分别称为品种家和品种乙）进行田间试验．选取两大块地，每大块地分成n小块地，在总共2n小块地中，随机选n小块地种植品种甲，另外n小块地种植品种乙．
（I）假设n=2，求第一大块地都种植品种甲的概率；
（II）试验时每大块地分成8小块，即n=8，试验结束后得到品种甲和品种乙在个小块地上的每公顷产量（单位：kg/hm2）如下表：
| 品种甲 |
403 |
397 |
390 |
404 |
388 |
400 |
412 |
406 |
| 品种乙 |
419 |
403 |
412 |
418 |
408 |
423 |
400 |
413 |
分别求品种甲和品种乙的每公顷产量的样本平均数和样本方差；根据试验结果，你认为应该种植哪一品种？
附：样本数据
的的样本方差
，其中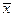
为样本平均数．
设
，函数
的图像与函数
的图像关于点
对称．
（1）求函数的解析式；
（2）若关于
的方程
有两个不同的正数解，求实数
的取值范围．
已知函数
的最大值为2．
（1）求函数
在
上的值域；
（2）已知
外接圆半径
，
，角A，B所对的边分别是a，b，求
的值．
提高大桥的车辆通行能力可改善整个城市的交通状况．一般情况下，大桥上的车流速度v(单位：千米/小时)是车流密度x(单位：辆/千米)的函数．当车流密度不超过50辆/千米时，车流速度为30千米/小时．研究表明：当50＜x≤200时，车流速度v与车流密度x满足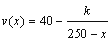
，当桥上的车流密度达到200辆/千米时，造成堵塞，此时车流速度为0千米/小时．
(Ⅰ) 当0<x≤200时，求函数v(x)的表达式；
(Ⅱ) 当车流密度x为多大时，车流量(单位时间内通过桥上观测点的车辆数，单位：辆/小时)f(x)＝x·v(x)可以达到最大，并求出最大值．(精确到个位，参考数据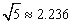
）
已知函数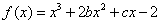
的图象在与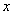
轴交点处的切线方程是
.
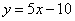(Ⅰ)求函数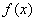
的解析式;
(Ⅱ)设函数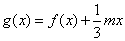
,若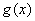
的极值存在,求实数
的取值范围以及当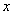取何值时函数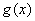分别取得极大和极小值.
已知
.
(Ⅰ) 若不等式
在区间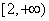
上恒成立，求实数
的取值范围;
(Ⅱ) 解关于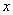
的不等式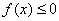
.