某花圃用花盆培育某种花苗，经过试验发现每盆的盈利与每盆的株数构成一定的关系，每盆植入3株时，平均单株盈利3元，以同样的栽培条件，若每盆增加1株，平均单株盈利就减少0.5元，要使每盆的盈利达到10元，每盆应该植多少株？
小明的解法如下：
解：设每盆花苗增加x株，则每盆花苗有（x+3）株，平均单株盈利为（3﹣0.5x）元，
由题意得（x+3）（3﹣0.5x）=10，
化简，整理得：x2﹣3x+=0
解这个方程，得：x1=1，x2=2，
答：要使每盆的盈利达到10元，每盆应该植入4株或5株．
（1）本题涉及的主要数量有每盆花苗株数，平均单株盈利，每盆花苗的盈利等，请写出两个不同的等量关系：_____________________________________________________,
_____________________________________________________________．
（2）请用一种与小明不相同的方法求解上述问题．
解方程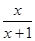
－
＝1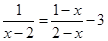
化简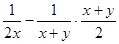
（1+
）÷
．
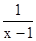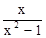解不等式组：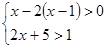
并把解集在数轴上表示出来。
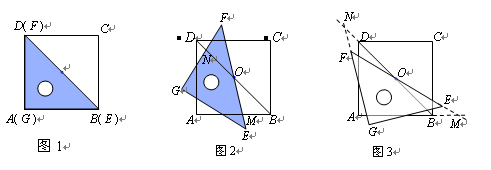
如图1，一等腰直角三角尺GEF（∠EGF=90°,∠GEF=∠GFE=45°,GE=GF）的两条直角边与正方形ABCD的两条边分别重合在一起．现正方形ABCD保持不动，将三角尺GEF绕斜边EF的中点O（点O也是BD中点）按顺时针方向旋转．如图2，当EF与AB相交于点M，GF与BD相交于点N时，通过观察或测量BM，FN的长度，猜想BM，FN相等吗？并说明理由；
若三角尺GEF旋转到如图3所示的位置时，线段FE的延长线与AB的延长线相交于点M，线段BD的延长线与GF的延长线相交于点N，此时，（1）中的猜想还成立吗？请说明理由．
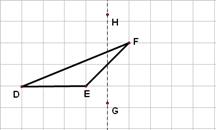
如图，在正方形网格上有一个△DEF。作△DEF关于直线HG的轴对称图形△ABC（不写作法）;
作EF边上的高（不写作法）;
若网格上的最小正方形边长为1，求△DEF的面积.
