某班数学兴趣小组有男生三名,分别记为 ,女生两名,分别记为
,女生两名,分别记为 ,现从中任选2名学生去参加校数学竞赛.
,现从中任选2名学生去参加校数学竞赛.
(1)写出这种选法的样本空间;
(2)求参赛学生中恰有一名男生的概率;
(3)求参赛学生中至少有一名男生的概率.
已知函数 在一个周期内的部分对应值如下表:
在一个周期内的部分对应值如下表:
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
(I)求 的解析式;
的解析式;
(II)设函数 ,
, ,求
,求 的最大值和最小值.
的最大值和最小值.
在某次综合素质测试中,共设有40个考室,每个考室30名考生.在考试结束后,为调查其测试前的培训辅导情况与测试成绩的相关性,抽取每个考室中座位号为05的考生,统计了他们的成绩,得到如图所示的频率分布直方图.
(Ⅰ)在这个调查采样中,用到的是什么抽样方法?
(Ⅱ)写出这40个考生成绩的众数、中位数(只写结果);
(Ⅲ)若从成绩在 的考生中任抽取2人,求成绩在
的考生中任抽取2人,求成绩在 的考生至少有一人的概率.
的考生至少有一人的概率.
已知等差数列 的前
的前 项和为
项和为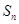 ,且
,且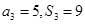 .
.
(I)求数列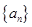 的通项公式;
的通项公式;
(II)设等比数列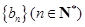 ,若
,若 ,求数列
,求数列 的前
的前 项和
项和 .
.
在平面直角坐标系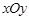 中,以坐标原点
中,以坐标原点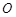 为极点,
为极点,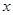 轴的非负半轴为极轴建立极坐标系.已知曲线
轴的非负半轴为极轴建立极坐标系.已知曲线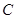 的极坐标方程为
的极坐标方程为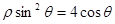 ,直线
,直线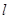 的参数方程为
的参数方程为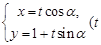 为参数,
为参数,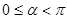 ).
).
(Ⅰ)化曲线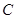 的极坐标方程为直角坐标方程;
的极坐标方程为直角坐标方程;
(Ⅱ)若直线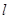 经过点
经过点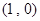 ,求直线
,求直线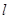 被曲线
被曲线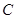 截得的线段
截得的线段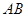 的长.
的长.
已知矩阵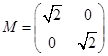 ,绕原点逆时针旋转
,绕原点逆时针旋转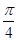 的变换所对应的矩阵为
的变换所对应的矩阵为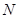 .
.
(Ⅰ)求矩阵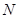 ;
;
(Ⅱ)若曲线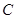 :
: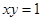 在矩阵
在矩阵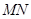 对应变换作用下得到曲线
对应变换作用下得到曲线 ,求曲线
,求曲线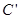 的方程.
的方程.