已知:如图,在四边形ABCD中,∠ABC=90°,CD⊥AD,AD2+CD2=2AB2.
(1)求证:AB=BC;
(2)当BE⊥AD于E时,试证明:BE=AE+CD.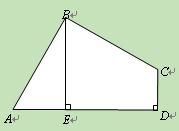
如图,在正方形ABCD中,CE⊥DF,求证:CE=DF.
如图,在△ABC中,AB=AC,点D是BC的中点,DE⊥AC于点E,DG⊥AB于点G,EK⊥AB于点K,GH⊥AC于点H、EK和GH相交于点F.
求证:GE与FD互相垂直平分.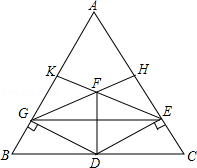
如图,在矩形ABCD中,对角线AC与BD相交于点O,AE垂直且平分线段BO,垂足为点E,BD=15cm,求AC、AB的长.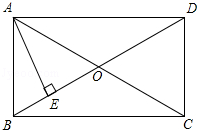
如图,在▱ABCD中,点E为CD的中点,连接BE并延长交AD的延长线于点F.求证:点E是BF的中点,点D是AF的中点.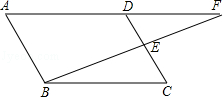
已知一个一次函数的图象与一个反比例函数的图象交于点P(﹣2,1)、Q(1,m).
(1)分别求出这两个函数的表达式.
(2)在同一平面直角坐标系中画出这两个函数的图象,根据图象回答,当x取何值时,一次函数的值大于反比例函数的值?