(本小题满分12分)
某医院计划从10名医生(7男3女)中选5人组成医疗小组下乡巡诊.
(I)设所选5人中女医生的人数为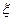 ,求
,求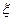 的分布列及数学期望;
的分布列及数学期望;
(II)现从10名医生中的张强、李军、王刚、赵永4名男医生,李莉、孙萍2名女医生共6人中选一正二副3名组长,在张强被选中的情况下,求李莉也被选中的概率.
已知椭圆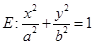
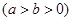 的左焦点为
的左焦点为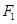 ,右焦点为
,右焦点为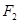 ,离心率
,离心率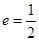 .过
.过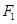 的直线交椭圆于
的直线交椭圆于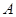 、
、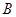 两点,且
两点,且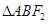 的周长为
的周长为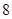 .
.
(1)求椭圆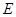 的方程;
的方程;
(2)设动直线 与椭圆
与椭圆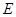 有且只有一个公共点
有且只有一个公共点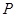 ,且与直线
,且与直线 相交于点
相交于点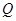 .求证:以
.求证:以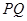 为直径的圆恒过一定点
为直径的圆恒过一定点 .并求出点
.并求出点 的坐标.
的坐标.
给定直线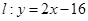 ,抛物线
,抛物线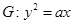
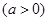
(1)当抛物线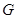 的焦点在直线
的焦点在直线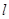 上时,求
上时,求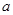 的值;
的值;
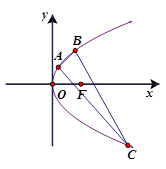
(2)若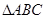 的三个顶点都在(1)所确定的抛物线
的三个顶点都在(1)所确定的抛物线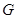 上,且点
上,且点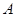 的纵坐标
的纵坐标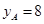 ,
,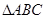 的重心恰是抛物线
的重心恰是抛物线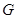 的焦点
的焦点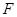 ,求直线
,求直线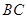 的方程.
的方程.
已知数列 的前
的前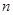 项和为
项和为 ,且
,且 ,
, ,数列
,数列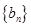 满足
满足
 .
.
(1)求 的表达式;
的表达式;
(2)求数列 的前
的前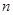 项和
项和 .
.
已知一圆经过点 ,
, ,且它的圆心在直线
,且它的圆心在直线 上.
上.
(1)求此圆的方程;
(2)若点 为所求圆上任意一点,且点
为所求圆上任意一点,且点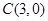 ,求线段
,求线段 的中点
的中点 的轨迹方程.
的轨迹方程.
(本小题满分13分)已知△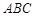 的两个顶点
的两个顶点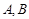 的坐标分别是
的坐标分别是 ,且
,且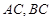 所在直线的斜率之积等于
所在直线的斜率之积等于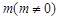 .
.
(1)求顶点 的轨迹
的轨迹 的方程,并判断轨迹
的方程,并判断轨迹 为何种曲线;
为何种曲线;
(2)当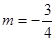 时,点
时,点 为曲线 C上点, 且点
为曲线 C上点, 且点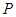 为第一象限点,过点
为第一象限点,过点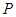 作两条直线与曲线C交于
作两条直线与曲线C交于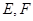 两点,直线
两点,直线 斜率互为相反数,则直线EF斜率是否为定值,若是,求出定值,若不是,请说明理由.
斜率互为相反数,则直线EF斜率是否为定值,若是,求出定值,若不是,请说明理由.