(本小题满分13分)已知△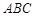 的两个顶点
的两个顶点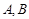 的坐标分别是
的坐标分别是 ,且
,且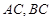 所在直线的斜率之积等于
所在直线的斜率之积等于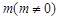 .
.
(1)求顶点 的轨迹
的轨迹 的方程,并判断轨迹
的方程,并判断轨迹 为何种曲线;
为何种曲线;
(2)当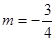 时,点
时,点 为曲线 C上点, 且点
为曲线 C上点, 且点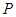 为第一象限点,过点
为第一象限点,过点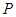 作两条直线与曲线C交于
作两条直线与曲线C交于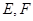 两点,直线
两点,直线 斜率互为相反数,则直线EF斜率是否为定值,若是,求出定值,若不是,请说明理由.
斜率互为相反数,则直线EF斜率是否为定值,若是,求出定值,若不是,请说明理由.
如图在直三棱柱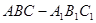 中,
中, .
.
(Ⅰ)求证: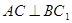 ;(Ⅱ)求二面角
;(Ⅱ)求二面角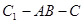 的余弦值大小;
的余弦值大小;
(Ⅲ)在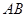 上是否存在点
上是否存在点 ,使得
,使得 ∥平面
∥平面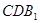 , 若存在,试给出证明;若不存在,请说明理由.
, 若存在,试给出证明;若不存在,请说明理由.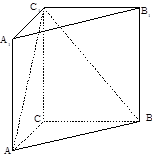
已知数列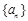 是首项为
是首项为 ,公比
,公比 的等比数列,设
的等比数列,设 ,数列
,数列 .
.
(1)求数列 的通项公式;(2)求数列
的通项公式;(2)求数列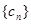 的前n项和Sn.
的前n项和Sn.
一袋子中有大小相同的2个红球和3个黑球,从袋子里随机取球,取到每个球的可能性是相同的,设取到一个红球得2分,取到一个黑球得1分。
(Ⅰ)若从袋子里一次随机取出3个球,求得4分的概率;
(Ⅱ)若从袋子里每次摸出一个球,看清颜色后放回,连续摸3次,求得分 的概率分布列及数学期望。
的概率分布列及数学期望。
△ABC中,a,b,c分别是角A,B,C的对边, ,且
,且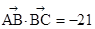 ,
,
(Ⅰ)求△ABC的面积;(Ⅱ)若a=7,求角∠C
已知函数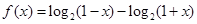 ,
,
(1)求函数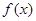 的定义域;
的定义域;
(2)判断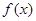 的奇偶性;
的奇偶性;
(3)方程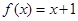 是否有根?如果有根
是否有根?如果有根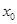 ,请求出一个长度为
,请求出一个长度为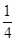 的区间
的区间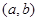 ,使
,使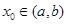 ;如果没有,请说明理由?(注:区间
;如果没有,请说明理由?(注:区间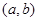 的长度
的长度 ).
).