(本小题满分12分)设命题 :实数
:实数 满足
满足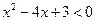 ,
, 实数
实数 满足
满足 ,若
,若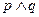 为真,求实数
为真,求实数 的取值范围.
的取值范围.
设函数 ,且关于x的不等式
,且关于x的不等式 的解集为
的解集为 ,
,
(1)求b的值;
(2)解关于x的不等式 (
( ).
).
已知 ,
, ,且
,且 ,
, ,
,
(1)求 ,
, ;
;
(2)求( )与
)与 的夹角.
的夹角.
(本题满分15分) 已知直线l1:x=my与抛物线C:y2=4x交于O (坐标原点),A两点,直线l2:x=my+m 与抛物线C交于B,D两 点.
点.
(Ⅰ) 若 | BD | = 2 | OA |,求实数m的值;
(Ⅱ) 过A,B,D分别作y轴的垂线,垂足分别为A1,B1,D1.记S1,S2分别为三角形OAA1和四 边形BB1D1D的面积,求
边形BB1D1D的面积,求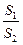 的取值范围.
的取值范围.
(本题满分15分) 已知实数a满足1<a≤2,设函数f (x)= x3-
x3-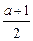 x2+ax.
x2+ax.
(Ⅰ) 当a=2时,求f (x)的极小值;
(Ⅱ) 若函数g(x)=4x3+3bx2-6(b+2)x (b∈R) 的极小值点与f (x)的极小值点相同,
求证:g(x)的极大值小于等于10.
(本题满分14分) 如图,在三棱柱BCD-B1C1D1与四棱锥A-BB1D1D的组合体中,已知BB1⊥平面BCD,四边形ABCD是平行四边形,∠ABC=120°,AB= ,AD=3,BB1=1.
,AD=3,BB1=1.
(Ⅰ) 设O是线段BD的中点,
求证:C1O∥平面AB1D1;
(Ⅱ) 求直线AB1与平面ADD1所成的角.