(本小题满分12分)已知椭圆
 经过点
经过点 ,一个焦点是
,一个焦点是 .
.
(Ⅰ)求椭圆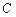 的方程;
的方程;
(Ⅱ)设椭圆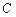 与
与 轴的两个交点为
轴的两个交点为 、
、 ,点
,点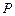 在直线
在直线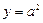 上,直线
上,直线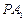 、
、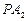 分别与椭圆
分别与椭圆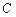 交于
交于 、
、 两点.试问:当点
两点.试问:当点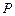 在直线
在直线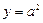 上运动时,直线
上运动时,直线 是否恒经过定点
是否恒经过定点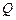 ?证明你的结论.
?证明你的结论.
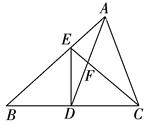 如右图,已知在△ABC中,D是BC边上的中点,且AD=AC,DE⊥BC,DE与AB相交于点E,EC与AD相交于点F.
如右图,已知在△ABC中,D是BC边上的中点,且AD=AC,DE⊥BC,DE与AB相交于点E,EC与AD相交于点F.
(1)求证:△ABC∽△FCD.
(2)若S△FCD=5,BC=10,求DE的长.
如右图所示,E为△ABC的边AC上一点,=,连结BE.
(1)若G为BE的中点,连结AG并延长交BC于D,求BD∶DC的值.
(2)若BG∶GE=2∶1,则BD∶DC的值将如何变化?
(3)若的值由改变为,G仍为BE中点,求BD∶DC.
已知直线l的参数方程:(t为参数)和圆C的极坐标方程:ρ=2sin(θ为参数).
(1)将直线l的参数方程和圆C的极坐标方程化为直角坐标方程;
(2)判断直线l和圆C的位置关系
已知P(x,y)是圆x2+y2=2y上的动点.
(1)求2x+y的取值范围;
(2)若x+y+c>0恒成立,求实数c的取值范围
已知直线l的极坐标方程为:ρcos=6,圆O的参数方程为:求直线l与圆O相交所得弦的弦长.