（本小题满分14分）(1）
（本小题满分7分）选修4-2：矩阵与变换
已知曲线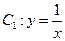
绕原点逆时针旋转
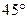后可得到曲线
，
（I）求由曲线
变换到曲线
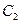对应的矩阵
；.
（II）若矩阵
，求曲线依次经过矩阵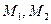
对应的变换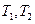
变换后得到的曲线方程.
（2）（本小题满分7分）选修4—4：坐标系与参数方程
已知直线
的参数方程为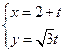
（t为参数），曲线C的极坐标方程为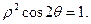
（1）求曲线C的直角坐标方程； （2）求直线被曲线C截得的弦长.
某单位最近组织了一次健身活动，活动分为登山组和游泳组，且每个职工至多参加了其中一组，在参加活动的职工中，青年人占42.5％，中年人占47.5％，
老年人占10％.登山组的职工占参加活动总人数的
，且该组中，青年人占50％，中年人占40％，老年人占10％。为了了解各组不同年龄层次的职工对本次活动的满意程度，现用分层抽样方法从参加活动的全体职工中抽取一个容量为200的样本，试确定
（Ⅰ）游泳组中，青年人、中年人、老年人分别所占的比例；
（Ⅱ）游泳组中，青年人、中年人、老年人分别应抽取的人数.
某种产品的广告费支出x与销售额y(单位：百万元)之间有如下对应数据：
| x |
2 |
4 |
5 |
6 |
8 |
| y |
30 |
40 |
50 |
60 |
70 |
如果y与x之间具有线性相关关系．
(1)求这些数据的线性回归方程；
(2)预测当广告费支出为9百万元时的销售额．
由四个不同数字1，2，4，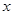
组成无重复数字的三位数，
⑴若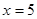
，其中能被5整除的共有多少个？
⑵若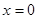
，其中的偶数共有多少个？
⑶若所有这些三位数的各位数字之和是252，求.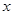
不等式选讲设函数
。
（Ⅰ）解不等式f（x）>2；
（Ⅱ）求函数y= f（x）的最小值。
在
中，内角
对边的边长分别是
，已知
，
．
（Ⅰ）若的面积等于
，求
；
（Ⅱ）若
，求的面积．