已知函数 是定义在
是定义在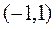 上的奇函数,且
上的奇函数,且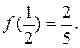
(1)确定函数 的解析式;
的解析式;
(2)判断并证明 在
在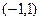 的单调性;
的单调性;
(3)解不等式
为了解某市民众对政府出台楼市限购令的情况,在该市随机抽取了50名市民进行调查,他们月收入(单位:百元)的频数分布及对楼市限购令赞成的人数如下表:
| 月收入 |
[15,25) |
[25,35) |
[35,45) |
[45,55) |
[55,65) |
[65,75] |
| 频数 |
5 |
10 |
15 |
10 |
5 |
5 |
| 赞成人数 |
4 |
8 |
12 |
5 |
2 |
1 |
将月收入不低于55的人群称为“高收入族”,月收入低于55的人群称为“非高收入族”.
(1)根据已知条件完成下面的2×2列联表,问能否在犯错误的概率不超过0.01的前提下认为非高收入族赞成楼市限购令?
| 非高收入族 |
高收入族 |
合计 |
|
| 赞成 |
|||
| 不赞成 |
|||
| 合计 |
(2)现从月收入在[15,25)的人群中随机抽取两人,求所抽取的两人都赞成楼市限购令的概率.
附:K2=
| P(K2≥k0) |
0.05 |
0.025 |
0.010 |
0.005 |
| k0 |
3.841 |
5.024 |
6.635 |
7.879 |
已知数列{an}的前n项和Sn=n2(n∈N*),等比数列{bn}满足b1=a1,2b3=b4.
(1)求数列{an}和{bn}的通项公式;
(2)若cn=an·bn(n∈N*),求数列{cn}的前n项和Tn.
已知函数f(x)=tan .
.
(1)求f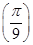 的值;
的值;
(2)设α∈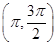 ,若f
,若f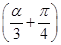 =2,求cos
=2,求cos 的值.
的值.
已知某地今年年初拥有居民住房的总面积为a(单位:m2),其中有部分旧住房需要拆除.当地有关部门决定每年以当年年初住房面积的10%建设新住房,同时也拆除面积为b(单位:m2)的旧住房.
(1)分别写出第1年末和第2年末的实际住房面积的表达式.
(2)如果第5年末该地的住房面积正好比今年年初的住房面积增加了30%,则每年拆除的旧住房面积b是多少?(计算时取1.15=1.6)
甲、乙两人用农药治虫,由于计算错误,在A,B两个喷雾器中分别配制成12%和6%的药水各10千克,实际要求两个喷雾器中的农药的浓度是一样的,现在只有两个能容纳1千克药水的药瓶,他们从A,B两个喷雾器中分别取1千克的药水,将A中取得的倒入B中,B中取得的倒入A中,这样操作进行了n次后,A喷雾器中药水的浓度为an%,B喷雾器中药水的浓度为bn%.
(1)证明an+bn是一个常数.
(2)求an与an-1的关系式.
(3)求an的表达式.