(本小题满分14分)
已知函数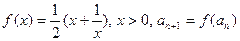 ,对于任意的
,对于任意的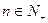 ,都有
,都有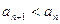 .
.
(Ⅰ)求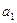 的取值范围;
的取值范围;
(Ⅱ)若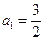 ,证明
,证明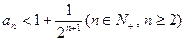 ;
;
(Ⅲ)在(Ⅱ)的条件下证明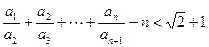 .
.
 在△ABC中,角A、B、C的对边分别为a、b、c.已知a+b=5,c=
在△ABC中,角A、B、C的对边分别为a、b、c.已知a+b=5,c=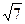 ,
,
且 .(1)求角C的大小;(2)求△ABC的面积.
.(1)求角C的大小;(2)求△ABC的面积.
在三棱锥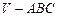 中,底面
中,底面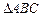 是以
是以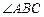 为直角的等腰三角形.又
为直角的等腰三角形.又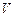 在底面
在底面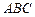 上的射影
上的射影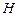 在线段
在线段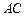 上且靠近点
上且靠近点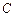 ,
,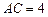 ,
,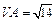 ,
, 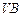 和底面
和底面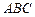 所成的角为
所成的角为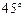 .
.
(Ⅰ)求点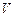 到底面
到底面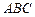 的距离;
的距离;
(Ⅱ)求二面角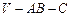 的大小的正切值.
的大小的正切值.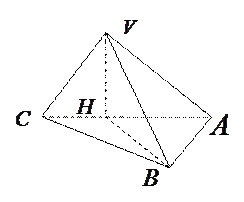
等比数列
的前
项和为
,已知对任意的
,点
,均在函数
且
均为常数)的图像上.
(1)求
的值;
(11)当
时,记
,证明:对任意的
,不等式
成立.
设函数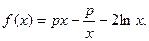
(Ⅰ)若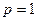 ,函数
,函数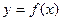 是否有极值,若有则求出极值,若没有,请说明理由.
是否有极值,若有则求出极值,若没有,请说明理由.
(Ⅱ)若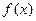 在其定义域内为单调函数,求实数p的取值范围.
在其定义域内为单调函数,求实数p的取值范围.
已知函数f(x)=x-ln(x+a)在x=1处取得极值.
(1)求实数a的值;
(2)若关于x的方程f(x)+2x=x2+b在[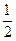 ,2]上恰有两个不相等的实数根,求实数b的取值范围;
,2]上恰有两个不相等的实数根,求实数b的取值范围;
(3)证明: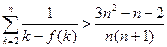 (n∈N,n≥2).参考数据:ln2≈0.6931.
(n∈N,n≥2).参考数据:ln2≈0.6931.