(本小题满分13分)(理科做)如图,在四棱锥P-ABCD中,已知PB⊥底面ABCD,BC⊥AB,AD∥BC,AB=AD=2,CD⊥PD,异面直线PA和CD所成角等于60°.
(1)求证:面PCD⊥面PBD;
(2)求直线PC和平面PAD所成角的正弦值的大小;
(3)在棱PA上是否存在一点E,使得二面角A-BE-D的余弦值为?若存在,指出点E在棱PA上的位置,若不存在,说明理由.
(文科做)己知函数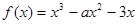
(1)若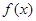 在区间
在区间 上是增函数,求实数
上是增函数,求实数 的取值范围;
的取值范围;
(2)若 是
是 的极值点,求
的极值点,求 在
在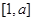 上的最大值;
上的最大值;
(3)在(2)的条件下,是否存在实数b,使得函数 的图象与函数
的图象与函数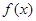 的图象恰有3个交点,若存在,请求出实数b的取值范围;若不存在,试说明理由
的图象恰有3个交点,若存在,请求出实数b的取值范围;若不存在,试说明理由
(本小题满分12分)
已知点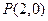 及圆
及圆 :
: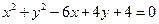 .
.
(1)若直线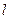 过点
过点 且与圆心
且与圆心 的距离为1,求直线
的距离为1,求直线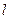 的方程;
的方程;
(2)设过点P的直线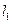 与圆
与圆 交于
交于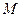 、
、 两点,当
两点,当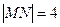 时,求以线段
时,求以线段 为直径的圆
为直径的圆 的方程;
的方程; (3)设直线
(3)设直线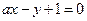 与圆
与圆 交于
交于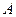 ,
, 两点,是否存在实数
两点,是否存在实数 ,使得过点
,使得过点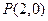 的直线
的直线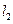 垂直平分弦
垂直平分弦 ?若存在,求出实数
?若存在,求出实数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(本小题满分12分)
如图,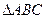 为正三角形,
为正三角形, 平面
平面 ,
, 是
是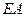 的中点,
的中点,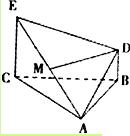
(1)求证:DM//面ABC;
(2)平面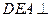 平面
平面 。
。
(3)求直线AD与面AEC所成角的正弦值;
.(本小题满分10分)
如图所示,在三棱锥 中,
中, ,且
,且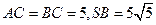 。
。
(1)证明: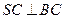 ;
;
(2)求侧面 与底面
与底面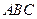 所成二面角的大小;
所成二面角的大小;
(本小题满分10分)
如图,矩形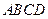 的两条对角线相交于点
的两条对角线相交于点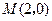 ,
, 边所在直线的方程为
边所在直线的方程为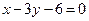 , 点
, 点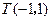 在
在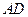 边所在直线上.
边所在直线上.
(1)求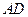 边所在直线的方程;
边所在直线的方程;
(2)求矩形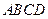 外接圆的方程
外接圆的方程 ;
;
(本小题满分8分)
如图,一个圆锥形的空杯子上面放着一个半球形的冰淇淋,如果冰淇淋融化了,冰淇淋会从杯子溢出吗?请用你的计算数据说明理 由.
由.
|