如图,AB是半径O的直径,AB=2.射线AM、BN为半圆O的切线.在AM上取一点D,连接BD交半圆于点C,连接AC.过O点作BC的垂线OE,垂足为点E,与BN相交于点F.过D点作半圆O的切线DP,切点为P,与BN相交于点Q.
(1)求证:△ABC∽△OFB;
(2)当△ABD与△BFO的面枳相等时,求BQ的长;
(3)求证:当D在AM上移动时(A点除外),点Q始终是线段BF的中点.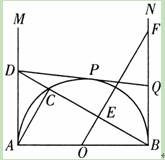
解不等式组: .
.
平面上,矩形ABCD与直径为QP的半圆K如图摆放,分别延长DA和QP交于点O,且∠BOQ=60°,OQ=OD=3,OP=2,OA=AB=1.让线段OD及矩形ABCD位置固定,将线段OQ连带着半圆K一起绕着点O按逆时针方向形如旋转,设旋转角为α(0°≤α≤60°).
发现(1)当α=0°,即初始位置时,点P____直线AB上.(填“在”或“不在”)求当α是多少时,OQ经过点B?
(2)在OQ旋转过程中.简要说明α是多少时,点P,A间的距离最小?并指出这个最小值:
(3)如图,当点P恰好落在BC边上时.求α及S阴影.
拓展如图.当线段OQ与CB边交于点M,与BA边交于点N时,设BM=x(x>0),用含x的代数式表示BN的长,并求x的取值范围.
探究当半圆K与矩形ABCD的边相切时,求sin α的值.
如图,已知点O(0,0),A(-5,0),B(2,1),抛物线l:y=-(x-h)2+1(h为常数)与y轴的交点为C.
(1)l经过点B,求它的解析式,并写出此时l的对称轴及顶点坐标:
(2)设点C的级坐标为yc,求yc的最大值,此时l上有两点(x1,y1),(x2,y2),其中x1>x2≥0,比较y1与y1的大小;
(3)当线段OA被l只分为两部分,且这两部分的比是1:4时,求h的值.
某厂生产A,B两种产品.其单价随市场变化而做相应调整.营销人员根据前三次单价变化的情况,绘制了如下统计表及不完整的折线图:
A,B产品单价变化统计表
| 第一次 |
第二次 |
第三次 |
|
| A产品单价(元/件) |
6 |
52 |
63.5 |
| B产品单价(元/件) |
3.5 |
4 |
3 |

并求得A产品三次单价的平均数和方差: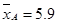 :
: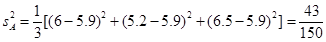 .
.
(1)补全图中B产品单价变化的折线图.B产品第三次的单价比上一次的单价降低了____%;
(2)求B产品三次单价的方差,并比较哪种产品的单价波动小:
(3)该厂决定第四次调价,A产品的单价仍为6.5元/件,B产品的单价比3元/件上调m%(m>0),使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1.求m的值.
水平放置的容器内原有210毫米高的水,如图.将若干个球逐一放入容器中,每放入一个大球水面就上升4毫米,每放入一个小球水面就上升3毫米,假定放入容器中的所有球完全浸没水中且水不溢出,设水面高为y毫米.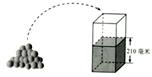
(1)只放入大球,且个数为x大,求y与x大的函数关系式(不必写出x大的范围);
(2)仅放入6个大球后,开始放入小球,且小球个数为x小.
①求y与x小的函数关系式(不必写出x小的范围);
②限定水面高不超过260毫米,最多放入几个小球?