(本小题满分14分)
如图,直二面角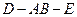 中,四边形
中,四边形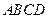 是正方形,
是正方形,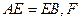 为CE上的点,且
为CE上的点,且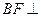 平面
平面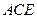 .
.
(1)求证: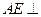 平面
平面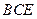 ;
;
(2)求二面角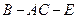 的余弦值.
的余弦值.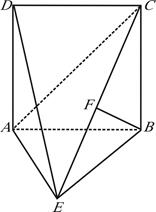
已知数列 的前n项和为
的前n项和为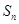 ,点
,点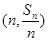 在直线
在直线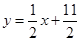 上.数列{bn}满足
上.数列{bn}满足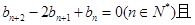
 ,前9项和为153.
,前9项和为153.
(Ⅰ)求数列 、
、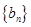 的通项公式;
的通项公式;
(Ⅱ)设 ,数列
,数列 的前n和为
的前n和为 ,求使不等式
,求使不等式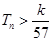 对一切
对一切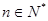 都成立的最大正整数k的值.
都成立的最大正整数k的值.
已知 且
且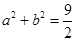 ,若
,若 恒成立,
恒成立,
(Ⅰ)求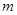 的最小值;
的最小值;
(Ⅱ)若 对任意的
对任意的 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
某货轮在A处看灯塔B在货轮的北偏东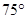 的方向上,距离为
的方向上,距离为 海里,在A处看灯塔C在货轮的北偏西
海里,在A处看灯塔C在货轮的北偏西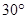 的方向上,距离为
的方向上,距离为 海里,货轮由A处向正北航行到D处时,再看灯塔B在南偏东
海里,货轮由A处向正北航行到D处时,再看灯塔B在南偏东 方向上,求:
方向上,求:
(1)AD的距离;
(2)CD的距离。
已知三个实数a、b、c成等差数列,且它们的和为12,又a+2、b+2、c+5成等比数列,求a、b、c的值。
已知 ,且
,且
(Ⅰ)求 的值.
的值.
(Ⅱ)求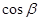 的值.
的值.