数学课堂上，徐老师出示一道试题：如图（十）所示，在正三角形A-优题课

数学课堂上，徐老师出示一道试题：如图（十）所示，在正三角形ABC中，M是BC边（不含端点B、C）上任意一点，P是BC延长线上一点，N是∠ACP的平分线上一点．若∠AMN＝60°，求证：AM＝MN．

(1)经过思考，小明展示了一种正确的证明过程．请你将证明过程补充完整．
证明：在AB上截取EA＝MC，连结EM，得△AEM．
∵∠1＝180°－∠AMB－∠AMN，∠2＝180°－∠AMB－∠B，∠AMN＝∠B＝60°，∴∠1＝∠2．
又CN平分∠ACP，∠4＝∠ACP＝60°．∴∠MCN＝∠3＋∠4＝120°…………①
又∵BA＝BC，EA＝MC，∴BA－EA＝BC－MC，即BE＝BM．
∴△BEM为等边三角形．∴∠6＝60°．
∴∠5＝180°－∠6＝120°．………②
∴由①②得∠MCN＝∠5．
在△AEM和△MCN中，
∵________________________________
∴△AEM≌△MCN (ASA)．∴AM＝MN．
(2)若将试题中的“正三角形ABC”改为“正方形A₁B₁C₁D₁”（如图），N₁是∠D₁C₁P₁的平分线上一点，则当∠A₁M₁N₁＝90°时，结论A₁M₁＝M₁N₁．是否还成立？（直接写出答案，不需要证明）
(3)若将题中的“正三角形ABC”改为“正多边形A_nB_nC_nD_n…X_n”，请你猜想：当∠A_nM_nN_n＝ °时，结论A_nM_n＝M_nN_n仍然成立？（直接写出答案，不需要证明）

科目数学题型解答题难度中等

知识点：圆内接四边形的性质

如图，在 $▱ ABCD$ 中，过 $B$ 点作 $BM ⊥ AC$ 于点 $E$ ，交 $CD$ 于点 $M$ ，过 $D$ 点作 $DN ⊥ AC$ 于点 $F$ ，交 $AB$ 于点 $N$ ．

（1）求证：四边形 $BMDN$ 是平行四边形；

（2）已知 $AF = 12$ ， $EM = 5$ ，求 $AN$ 的长．

抛物线 $y = 4 x^{2} - 2 ax + b$ 与 $x$ 轴相交于 $A (x_{1}$ ， $0)$ ， $B (x_{2}$ ， $0) (0 < x_{1} < x_{2})$ 两点，与 $y$ 轴交于点 $C$ ．

（1）设 $AB = 2$ ， $\tan ∠ ABC = 4$ ，求该抛物线的解析式；

（2）在（1）中，若点 $D$ 为直线 $BC$ 下方抛物线上一动点，当 $ΔBCD$ 的面积最大时，求点 $D$ 的坐标；

（3）是否存在整数 $a$ ， $b$ 使得 $1 < x_{1} < 2$ 和 $1 < x_{2} < 2$ 同时成立，请证明你的结论．

如图1，在平面直角坐标系， $O$ 为坐标原点，点 $A (- 1, 0)$ ，点 $B (0, \sqrt{3})$ ．

（1）求 $∠ BAO$ 的度数；

（2）如图1，将 $ΔAOB$ 绕点 $O$ 顺时针旋转得△ $A' OB'$ ，当 $A'$ 恰好落在 $AB$ 边上时，设△ $AB' O$ 的面积为 $S_{1}$ ，△ $BA' O$ 的面积为 $S_{2}$ ， $S_{1}$ 与 $S_{2}$ 有何关系？为什么？

（3）若将 $ΔAOB$ 绕点 $O$ 顺时针旋转到如图2所示的位置， $S_{1}$ 与 $S_{2}$ 的关系发生变化了吗？证明你的判断．

【探究函数 y = x + 4 x 的图象与性质】

（1）函数 $y = x + \frac{4}{x}$ 的自变量 $x$ 的取值范围是　　；

（2）下列四个函数图象中函数 $y = x + \frac{4}{x}$ 的图象大致是　　；

（3）对于函数 $y = x + \frac{4}{x}$ ，求当 $x > 0$ 时， $y$ 的取值范围．

请将下列的求解过程补充完整．

解： $∵ x > 0$

$∴ y = x + \frac{4}{x} = {(\sqrt{x})}^{2} + {(\frac{2}{\sqrt{x}})}^{2} = {(\sqrt{x} - \frac{2}{\sqrt{x}})}^{2} +$ 　　

$∵ {(\sqrt{x} - \frac{2}{\sqrt{x}})}^{2} ⩾ 0$

$∴ y ⩾$ 　　．

$[$ 拓展运用 $]$

（4）若函数 $y = \frac{x^{2} - 5 x + 9}{x}$ ，则 $y$ 的取值范围　　．

某校在一次大课间活动中，采用了四种活动形式： $A$ 、跑步， $B$ 、跳绳， $C$ 、做操， $D$ 、游戏．全校学生都选择了一种形式参与活动，小杰对同学们选用的活动形式进行了随机抽样调查，根据调查统计结果，绘制了不完整的统计图．

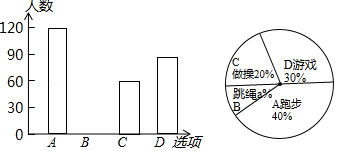
请结合统计图，回答下列问题：

（1）本次调查学生共　　人， $a =$ 　　，并将条形图补充完整；

（2）如果该校有学生2000人，请你估计该校选择“跑步”这种活动的学生约有多少人？

（3）学校让每班在 $A$ 、 $B$ 、 $C$ 、 $D$ 四种活动形式中，随机抽取两种开展活动，请用树状图或列表的方法，求每班抽取的两种形式恰好是“跑步”和“跳绳”的概率．