某课题学习小组在一次活动中对三角 形的内接正方形的有关问题进行了探讨:
形的内接正方形的有关问题进行了探讨:
定义:如果一个正方形的四个顶点都在一个三角形的边上,那么我们就把这个正方形叫做三角形的内接正方形.
结论:在探讨过程中,有三位同学得出如下结果:
甲同学:在钝角、直角、不等边锐角三角形中分别存在____个、________个、________个大小不同的内接正方形.
乙同学:在直角三角形中,两个顶点都在斜边上的内接正方形的面积较大.
丙同学:在不等边锐角三角形中,两个顶点都在较大边上的内接正方形的面积反而较小.
任务:(1)填充甲同学结论中的数据;
(2)乙 同学的结果正确吗?若不正确,请举出一个反例并通过计算给予说明,若正确,请给出证明;
同学的结果正确吗?若不正确,请举出一个反例并通过计算给予说明,若正确,请给出证明;
(3)请你结合(2)的判定,推测丙同学的结论是否正确,并证明
(如图,设锐角△AB C的三条边分别为
C的三条边分别为 不妨设
不妨设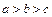 ,三条边上的对应高分别为
,三条边上的对应高分别为 ,内接正方形的边长分别为
,内接正方形的边长分别为 .若你对本小题证明有困难,可直接用
.若你对本小题证明有困难,可直接用 “
“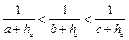 ”这个结论,但在证明正确的情况下扣1分).
”这个结论,但在证明正确的情况下扣1分).
(10分) 如图,Rt△ABC中,∠C = 90°,把Rt△ABC绕着B点逆时针旋转,得到Rt△DBE,点E在AB上.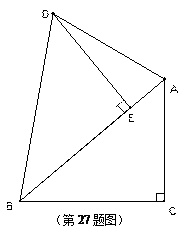
(1)若∠BDA = 70°,求∠BAC的度数.
(2)若BC = 8,AC = 6,求△ABD中AD边上的高.
(10分) 铭润超市用5000元购进一批新品种的苹果进行试销,由于销售状况良好,超市又调拨11000元资金购进该品种苹果,但这次的进货价比试销时每千克多了0.5元,购进苹果数量是试销时的2倍.
(1)试销时该品种苹果的进货价是每千克多少元?
(2)如果超市将该品种苹果按每千克7元的定价出售,当大部分苹果售出后,余下的400千克按定价的七折(“七折”即定价的70%)售完,那么超市在这两次苹果销售中共盈利多少元?
(12分) 如图,在△ABC中,ME和NF分别垂直平分AB和AC.
(1)若BC =" 10" cm,试求△AMN的周长.
(2)在△ABC中,AB = AC,∠BAC = 100°,求∠MAN的度数.
(3) 在 (2) 中,若无AB = AC的条件,你还能求出∠MAN的度数吗?若能,请求出;若不能,请说明理由.
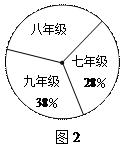
(10分) 阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.1995年联合国教科文组织把每年4月23日确定为“世界读书日”.表(1)是该校学生阅读课外书籍情况统计表,图2是某校三个年级学生人数分布扇形统计图,其中八年级人数为408人.请你根据图表中的信息,解答下列问题:
|
(10分) 如图,在方格纸(每个小正方形边长为1)中,先把梯形ABCD向左平移6个单位长度得到梯形A1B1C1D1.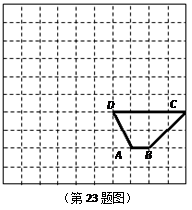
(1)请你在方格纸中画出梯形A1B1C1D1 ;
(2)以点C1为旋转中心,把 (1) 中画出的梯形绕点C1顺时针方向旋转 得到梯形A2B2C2D2,请你画出梯形A2B2C2D2.
得到梯形A2B2C2D2,请你画出梯形A2B2C2D2.