(本小题满分12分)(1)对于定义在 上的函数
上的函数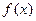 ,满足
,满足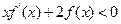 ,求证:函数
,求证:函数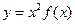 在
在 上是减函数;
上是减函数;
(2)请你认真研读(1)中命题并联系以下命题:若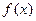 是定义在
是定义在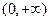 上的可导函数,满足
上的可导函数,满足 ,则
,则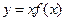 是
是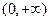 上的减函数。然后填空建立一个普遍化的命题
上的减函数。然后填空建立一个普遍化的命题 :
:
设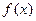 是定义在
是定义在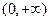 上的可导函数,
上的可导函数, ,若
,若  +
+
 ,
,
则 是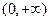 上的减函数。
上的减函数。
注:命题的普遍化就是从考虑一个对象过渡到考虑包含该对象的一个集合;或者从考虑一个较小的集合过渡到考虑包含该较小集合的更大集合。
(3)证明(2)中建立的普遍化命题。
已知函数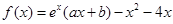 ,曲线
,曲线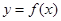 在点
在点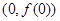 处切线方程为
处切线方程为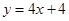 .
.
(Ⅰ)求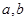 的值;
的值;
(Ⅱ)讨论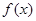 的单调性,并求
的单调性,并求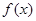 的极大值.
的极大值.
已知点 ,圆
,圆 :
: ,过点
,过点 的动直线
的动直线 与圆
与圆 交于
交于 两点,线段
两点,线段 的中点为
的中点为 ,
, 为坐标原点.
为坐标原点.
(1)求 的轨迹方程;
的轨迹方程;
(2)当 时,求
时,求 的方程及
的方程及 的面积.
的面积.
如图,三棱柱 中,
中, ,
, ,
, .
.
(1)证明: ;
;
(2)若 ,
, ,求三棱柱
,求三棱柱 的体积.
的体积.
从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量表得如下频数分布表:
| 质量指标值分组 |
[75,85) |
[85,95) |
[95,105) |
[105,115) |
[115,125) |
| 频数 |
6 |
26 |
38 |
22 |
8 |
(1)在答题卡上作出这些数据的频率分布直方图:
(2)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表);
(3)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定?
已知等差数列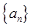 的公差
的公差 =1,前
=1,前 项和为
项和为 .
.
(1)若
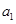 ;
;
(2)若 .
.