在平面直角坐标系中，已知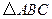
三个顶点的坐标分别为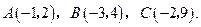
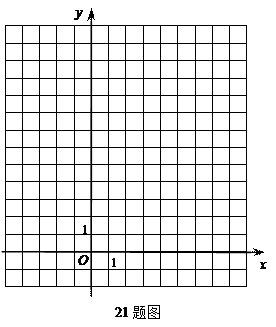
（1）画出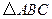，并求出
所在直线的解析式。
（2）画出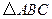绕点
顺时针旋转
后得到的
，并求出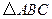在上述旋转过程中扫过的面积。
请阅读材料：
（1）如图1，在等边三角形ABC内有一点P，且PA=2，PB=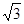
，PC=1．求∠BPC的度数和等边三角形ABC的边长.
李明同学的思路是：将△BPC绕点B顺时针旋转60°，画出旋转后的图形（如图2）．连接PP′.根据李明同学的思路，进一步思考后可求得∠BPC=_____°，等边△ABC的边长为_____.
（2）请你参考李明同学的思路，探究并解决下列问题：如图3，在正方形ABCD内有一点P，且PA=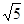
，BP=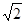
，PC=1．求∠BPC的度数和正方形ABCD的边长．
观察下列各式：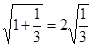
；
；
……，
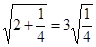请你猜想：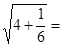
_______，
.
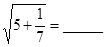计算（请写出推导过程）：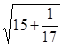
请你将猜想到的规律用含有自然数n（n≥1）的代数式表达出来：
_______________________________________________________
（本题8分）如图，在△ABC中，AB=AC，点D、E、F分别在AB、BC、AC边上，且BE=CF，BD=CE.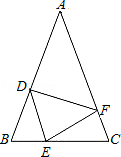
（1）求证：△DEF是等腰三角形；
（2）当∠A=40°时，求∠DEF的度数；
如图，在△ABC中，AB=AC，AD平分∠BAC．求证：∠DBC=∠DCB．
已知在△ABC中，AB、BC、AC三边长分别为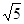
、
、
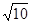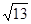，请你在下面的网格（每个小正方形边长为1）中画出格点三角形ABC（△ABC三个顶点都在小正方形的顶点处）．
（1）图中你画的△ABC的面积=______，
（2）计算△ABC中AB边上的高．