我州鼓苦荞茶、青花椒、野生蘑菇，为了让这些珍宝走出大山，走向世界，州政府决定组织21辆汽车装运这三种土特产共120吨，参加全国农产品博览会。现有A型、B型、C型三种汽车可供选择。已知每种型号汽车可同时装运2种土特产，且每辆车必须装满。根据下表信息，解答问题。
| |
 |
苦荞茶 |
青花椒 |
野生蘑菇 |
|
| 每 辆 汽 车 运 载 量 |
（吨） |
A型 |
 2 |
2 |
|
| B型 |
4 |
|
2 |
||
| C型 |
|
1 |
6 |
||
| 车型 |
A |
B |
C |
| 每辆车运费（元） |
1500 |
1800 |
2000 |
（1） 设A型汽车安排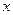
辆，B 型汽车安排
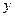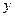辆，求与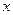之间的函数关系式。
（2） 如果三种型号的汽车都不少于4辆，车辆安排有几种方案？并写出每种方案。
（3） 为节约运费，应采用（2）中哪种方案？并求出最少运费。
如图，已知AB⊥BD，CD⊥BD．
（1）若AB＝16，CD＝9，BD＝15，请问在BD上是否存在P点，使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似？若存在，求BP的长；若不存在，请说明理由；
（2）若AB＝16，CD＝9，BD＝24，请问在BD上存在多少个P点，使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似？并求BP的长；
（3）若AB＝m，CD＝n，BD＝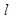
，请问在m、n、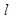满足什么关系时，存在以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似的三个P点?
（本小题满分8分）如图，点P是正方形ABCD内一点，点P到点A，B和D的距离分别为1，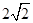
，
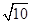．△ADP沿点A旋转至△ABP’，连结PP’，并延长AP与BC相交于点Q．
（1）求证：△APP’是等腰直角三角形；
（2）求∠BPQ的大小；
（3）求CQ的长．
（本小题满分6分）如图，△ABC中，CD是边AB上的高，且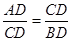
．
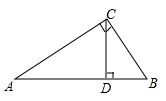
（1）求证：△ACD∽△CBD；
（2）求∠ACB的大小．
（本小题满分8分）如图，已知锐角△ABC（1）过点A作BC边的垂线MN，交BC于点D（用尺规作图法，保留作图痕迹，不要求写作法）；（2）在（1）条件下，若BC=5，AD=4， tan∠BAD=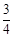
，求DC的长．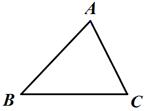
如图在Rt△ABC中，∠ACB=90°，D是边AB的中点，BE⊥CD，垂足为点E．已知AC=15，cosA=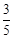
．
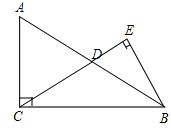
（1）求线段CD的长；
（2）求sin∠DBE的值．