(本小题满分8分)如图,点P是正方形ABCD内一点,点P到点A,B和D的距离分别为1,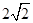 ,
,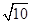 .△ADP沿点A旋转至△ABP’,连结PP’,并延长AP与BC相交于点Q.
.△ADP沿点A旋转至△ABP’,连结PP’,并延长AP与BC相交于点Q.
(1)求证:△APP’是等腰直角三角形;
(2)求∠BPQ的大小;
(3)求CQ的长.
(本题10分)
(1)计算:(-2015)0 ×|-3|-32+ ;
;
(2)解方程: -
- = 2.
= 2.
二次函数 的图象经过点(﹣1,4),且与直线
的图象经过点(﹣1,4),且与直线 相交于A、B两点(如图),A点在y轴上,过点B作BC⊥x轴,垂足为点C(﹣3,0).
相交于A、B两点(如图),A点在y轴上,过点B作BC⊥x轴,垂足为点C(﹣3,0).
(1)求二次函数的表达式;
(2)点N是二次函数图象上一点(点N在AB上方),过N作NP⊥x轴,垂足为点P,交AB于点M,求MN的最大值;
(3)在(2)的条件下,点N在何位置时,BM与NC相互垂直平分?并求出所有满足条件的N点的坐标.
如图,AB是⊙O的直径,OD垂直于弦AC于点E,且交⊙O于点D,F是BA延长线上一点,若∠CDB=∠BFD.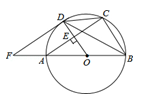
(1)求证:FD是⊙O的一条切线;
(2)若AB=10, AC=8,求DF的长.
如图,一楼房AB后有一假山,其坡度为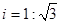 ,山坡坡面上E点处有一休息亭,测的假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
,山坡坡面上E点处有一休息亭,测的假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)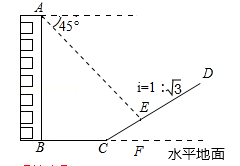
如图,在△ABC中,D,E分别是AB,AC的中点,过点E作EF∥AB,交BC于点F.
(1)求证:四边形DBFE是平行四边形;
(2)当△ABC满足什么条件时,四边形DBFE是菱形?为什么?