如图,一楼房AB后有一假山,其坡度为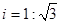 ,山坡坡面上E点处有一休息亭,测的假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
,山坡坡面上E点处有一休息亭,测的假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)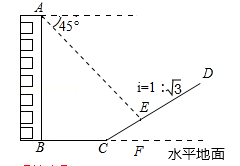
解不等式组 ,并把其解集在数轴上表示出来.
,并把其解集在数轴上表示出来.
解方程组: .
.
如图,AD∥BC,∠A=90°,E是AB上的一点,且AD=BE,∠1=∠2.
(1)Rt△ADE与Rt△BEC全等吗?请写出必要的推理过程;
(2)△CED是不是直角三角形?请说明理由;
(3)若已知AD=6,AB=14,请求出请求出△CED的面积.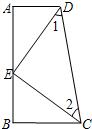
在一次数学活动中,黑板上画着如图所示的图形,活动前刘老师在准备的四张纸片上分别写有如下四个等式中的一个等式:
①AB=DC;②∠ABE=∠DCE;③AE=DE;④∠A=∠D
小明同学闭上眼睛从四张纸片中随机抽取一张,再从剩下的纸片中随机抽取另一张.请结合图形解答下列两个问题:
(1)请你写出在抽取的两张纸片上的等式为条件不能判断△BCE是等腰三角形的所有情形:
;(用序号表示)
(2)当抽得①和②时,用①,②作为条件能判定△BCE是等腰三角形吗?说说你的理由;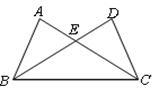
腾蛟人本超市欲招聘收银员一名,对A、B、C三名候选人进行了三项素质测试,各项测试成绩满分均为100分,根据结果择优录用.三位候选人的各项测试成绩如表所示: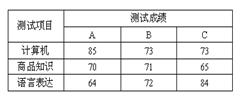
(1)如果根据三项测试的平均成绩确定录用人选,那么谁将被录用,说明理由;
(2)人本集团根据实际需要,将计算机、商品知识和语言表达能力测试得分按5:3:2的比例确定每人的成绩,此时谁将被录用?请写出推理过程。