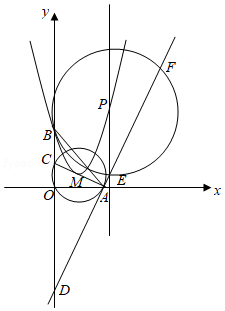
如图,在平面直角坐标系中,为坐标原点,点,点,的中线与轴交于点,且经过,,三点.
(1)求圆心的坐标;
(2)若直线与相切于点,交轴于点,求直线的函数表达式;
(3)在(2)的条件下,在过点且以圆心为顶点的抛物线上有一动点,过点作轴,交直线于点.若以为半径的与直线相交于另一点.当时,求点的坐标.
计算:
计算:
如图,动点A从原点出发向数轴负方向运动,同时动点B也从原点出发向数轴正方向运动,2秒后,两点相距16个单位长度.已知动点A、B的速度比为1∶3(速度单位:1个单位长度/秒).
(1)求两个动点运动的速度;
(2)在数轴上标出A、B两点从原点出发运动2秒时的位置;
(3)若表示数0的点记为O,A、B两点分别从(2)中标出的位置同时向数轴负方向运动,再经过多长时间,
OB=2OA.
如图,圆上有五个点,这五个点将圆分成五等份(每一份称为一段弧长),把这五个点按顺时针方向依次编号为1,2,3,4,5,若从某一点开始,沿圆周顺时针方向行走,点的编号是数字几,就走几段弧长,则称这种走法为一次“移位”.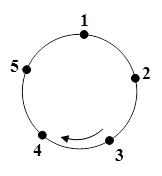
如:小明在编号为3的点,那么他应走3段弧长,即从3→ 4→5→1为第一次“移位”,这时他到达编号为1的点,然后从1→2为第二次“移位”.
(1)①若小明从编号为3的点开始,第三次“移位”后,他到达编号为_____的点;
②若小明从编号为4的点开始,第一次“移位”后,他到达编号为______的点,
若小明从编号为4的点开始,第四次“移位”后,他到达编号为______的点,
第2012次“移位”后,他到达编号为_______的点.
(2)若将圆进行二十等份,按照顺时针方向依次编号为1,2,3,…,20,小明从编号为3的点开始,沿顺
时针方向行走,经过60次“移位”后,他到达编号为_____的点.
学校组织春游,需租用汽车若干辆,如果每辆汽车坐40人,则有20人没有上车;如果每辆汽车坐45人,则可空出一辆汽车,并且有一辆车还可坐10人。问有多少辆汽车?共有多少名学生?