如图，正方形ABCD的边CD在正方形ECGF的边CE上，连接-优题课

题文

如图，正方形 $ABCD$ 的边 $CD$ 在正方形 $ECGF$ 的边 $CE$ 上，连接 $DG$ ，过点 $A$ 作 $AH / / DG$ ，交 $BG$ 于点 $H$ ．连接 $HF$ ， $AF$ ，其中 $AF$ 交 $EC$ 于点 $M$ ．

（1）求证： $ΔAHF$ 为等腰直角三角形．

（2）若 $AB = 3$ ， $EC = 5$ ，求 $EM$ 的长．

科目数学题型解答题难度中等

知识点：平行线分线段成比例平行四边形的判定与性质全等三角形的判定与性质正方形的性质

登录免费查看答案和解析

相关试题

如图，海中一小岛上有一个观测点A，某天上午9：00观测到某渔船在观测点A的西南方向上的B处跟踪鱼群由南向北匀速航行．当天上午9：30观测到该渔船在观测点A的北偏西60°方向上的C处．若该渔船的速度为每小时30海里，在此航行过程中，问该渔船从B处开始航行多少小时，离观测点A的距离最近？（计算结果用根号表示，不取近似值）．

某小区为了绿化环境，计划分两次购进A、B两种花草，第一次分别购进A、B两种花草30棵和15棵，共花费675元；第二次分别购进A、B两种花草12棵和5棵．两次共花费940元（两次购进的A、B两种花草价格均分别相同）．
（1）A、B两种花草每棵的价格分别是多少元？
（2）若购买A、B两种花草共31棵，且B种花草的数量少于A种花草的数量的2倍，请你给出一种费用最省的方案，并求出该方案所需费用．

小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况，他从中随机调查了50户居民的月均用水量（单位：t），并绘制了样本的频数分布表和频数分布直方图（如图）．

（1）请根据题中已有的信息补全频数分布表和频数分布直方图；

（2）如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭，请你通过样本估计总体中的中等用水量家庭大约有多少户？
（3）从月均用水量在2≤x＜3，8≤x＜9这两个范围内的样本家庭中任意抽取2个，求抽取出的2个家庭来自不同范围的概率．

化简：．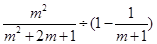

如图，AC=AE，∠1=∠2，AB=AD．求证：BC=DE．

试卷网试题网古诗词网作文网范文网