我州鼓苦荞茶、青花椒、野生蘑菇,为了让这些珍宝走出大山,走向世界,州政府决定组织21辆汽车装运这三种土特产共120吨,参加全国农产品博览会。现有A型、B型、C型三种汽车可供选择。已知每种型号汽车可同时装运2种土特产,且每辆车必须装满。根据下表信息,解答问题。
| |
 |
苦荞茶 |
青花椒 |
野生蘑菇 |
|
| 每 辆 汽 车 运 载 量 |
(吨) |
A型 |
 2 2 |
2 |
|
| B型 |
4 |
|
2 |
||
| C型 |
|
1 |
6 |
| 车型 |
A |
B |
C |
| 每辆车运费(元) |
1500 |
1800 |
2000 |
(1) 设A型汽车安排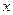 辆,B 型汽车安排
辆,B 型汽车安排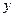 辆,求
辆,求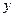 与
与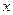 之间的函数关系式。
之间的函数关系式。
(2) 如果三种型号的汽车都不少于4辆,车辆安排有几种方案?并写出每种方案。
(3) 为节约运费,应采用(2)中哪种方案?并求出最少运费。
已知:线段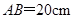 .
.
(1)如图,点 沿线段
沿线段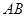 自
自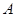 点向
点向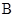 点以
点以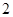 厘米/秒运动,点
厘米/秒运动,点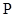 出发
出发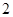 秒后,点
秒后,点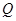 沿线段
沿线段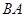 自
自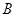 点向
点向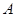 点以
点以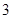 厘米/秒运动,问再经过几秒后
厘米/秒运动,问再经过几秒后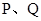 相距
相距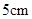 ?
?
(2)如图: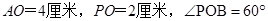 ,点
,点 绕着点
绕着点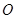 以
以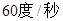 的速度逆时针旋转一周停止,同时点
的速度逆时针旋转一周停止,同时点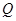 沿直线
沿直线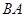 自
自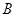 点向
点向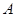 点运动,假若点
点运动,假若点 两点能相遇,求点
两点能相遇,求点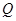 运动的速度 .
运动的速度 .
已知同一平面内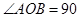 °,
°,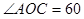 °,
°,
(1)填空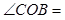 ;
;
(2)如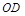 平分∠BOC,
平分∠BOC, 平分∠AOC,直接写出∠DOE的度数为°;
平分∠AOC,直接写出∠DOE的度数为°;
(3)试问在(2)的条件下,如果将题目中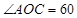 °改成
°改成 ,其他条件不变,你能求出∠DOE的度数吗?若能,请你写出求解过程;若不能,请说明理由.
,其他条件不变,你能求出∠DOE的度数吗?若能,请你写出求解过程;若不能,请说明理由.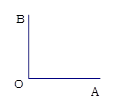
古运河是扬州的母亲河,为打造古运河风光带,现有一段河道整治任务由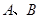 两工程队完成.
两工程队完成.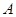 工程队单独整治该河道要16天才能完成;
工程队单独整治该河道要16天才能完成; 工程队单独整治该河道要24天才能完成.现在A工程队单独做6天后,B工程队加入合做完成剩下的工程,问A工程队一共做了多少天?
工程队单独整治该河道要24天才能完成.现在A工程队单独做6天后,B工程队加入合做完成剩下的工程,问A工程队一共做了多少天?
(1)根据题意,万颖、刘寅两名同学分别列出尚不完整的方程如下:
万颖: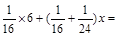

刘寅: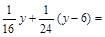 1
1
根据万颖、刘寅两名同学所列的方程,请你分别指出未知数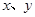 表示的意义,然后在,然后在方框中补全万颖同学所列的方程:
表示的意义,然后在,然后在方框中补全万颖同学所列的方程:
万颖: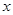 表示________________,刘寅:
表示________________,刘寅: 表示________________,万颖同学所列不完整的方程中的方框内该填.
表示________________,万颖同学所列不完整的方程中的方框内该填.
(2)求A工程队一共做了多少天.(写出完整的解答过程)
(1)由大小相同的小立方块搭成的几何体如图,请在下图的方格中画出该几何体的俯视图和左视图;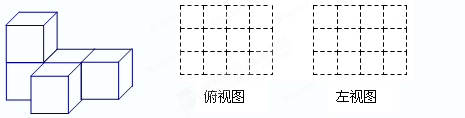
(2)用小立方体重新搭一几何体,使得它的俯视图和左视图与你在上图方格中所画的图一致,则搭建这样的新几何体最少要_______个小立方块,最多要_______个小立方块;
(3)如图是教师每天在黑板上书写用的粉笔,请画出图示粉笔俯视图.
回答下列问题:
(1)如图所示的甲、乙两个平面图形能折什么几何体?
(2)由多个平面围成的几何体叫做多面体.若一个多面体的面数为 ,顶点个数为
,顶点个数为 ,棱数为
,棱数为 ,分别计算第(1)题中两个多面体的
,分别计算第(1)题中两个多面体的 的值?你发现什么规律?
的值?你发现什么规律?
(3)应用上述规律解决问题:一个多面体的顶点数比面数大8,且有50条棱,求这个几何体的面数.