（11·珠海）（本题
满分7分）某校为庆祝国庆节举办游园活动，小军来到摸球
兑奖活动场地，李老师对小军说：“这里有A、B两个盒子，里面都装有一些乒乓球，你只
能选择在其中一只盒子中摸球．”获将规则如下：在A盒中有白色乒乓球4个，红色乒乓球
2个，一人只能摸一次且一次摸出一个球，若为红球则可获得玩具熊一个，否则不得奖；在
B盒中有白色乒乓球2个，红色乒乓球2个，一人只能摸一次且一次摸出两个球，若两球均
为红球则可获得玩具熊一个，否则不得奖．请问小军在哪只盒子内摸球获得玩具熊的机会更
大？说明你的理由．
如图，在直角梯形ABCD中,AD∥CB, 
,动点P从点D出发,沿射线DA的方向以每秒2个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒一个单位长的速度向点B运动,点P,Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t（秒）.
（1）设△BPQ的面积为S,求S与t之间的函数关系式;
（2）当t为何值时,四边形ABQP是平行四边形.
（3）当t为何值时,以B,P,Q三点为顶点的三角形是等腰三角形?
如图，已知直角梯形ABCD中，AD∥BC，AB⊥BC，AD＝2，AB＝8，CD＝10．
（1）求梯形ABCD的面积；
（2）动点P从点B出发，以2个单位/s的速度沿B→A→D→C方向向点C运动；动点Q从点C出发，以2个单位/s的速度沿C→D→A方向向点A运动；过点Q作QE⊥BC于点E．若P、Q两点同时出发，当其中一点到达终点时另一点也随之停止运动，设运动时间为t秒．问：
①当点P在B→A上运动时，是否存在这样的t，使得直线PQ将梯形ABCD的周长平分？若存在，请求出t的值，并判断此时PQ是否平分梯形ABCD的面积；若不存在，请说明理由．
②在运动过程中，是否存在这样的t，使得以P、D、Q为顶点的三角形恰好是以DQ为一腰的等腰三角形？若存在，请求出所有符合条件的t的值；若不存在，请说明理由．
如图，在矩形ABCD中，AB＝12cm，BC＝8cm．点E、F、G分别从点A、B、C同时出发，沿矩形的边按逆时针方向移动，点E、G的速度均为2cm/s，点F的速度为4cm/s，当点F追上点G（即点F与点G重合）时，三个点随之停止移动．设移动开始后第ts时，△EFG的面积为Scm2。
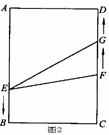
（1）当
＝1s时，S的值是多少？
（2）当
时，点E、F、G分别在边AB、BC、CD上移动，用含t的代数式表示S；当
时，点E在边AB上移动，点F、G都在边CD上移动，用含t的代数式表示S.
（3）若点F在矩形的边BC上移动，当为何值时，以点B、E、F为顶点的三角形与以C、F、G为顶点的三角形相似？请说明理由
如图所示，直线l：y=3x+3与x轴交于点A，与y轴交于点B．把△AOB沿y轴翻折，点A落到点C，抛物线过点B、C和D（3，0）．
（1）求直线BD和抛物线的解析式．
（2）若BD与抛物线的对称轴交于点M，点N在坐标轴上，以点N、B、D为顶点的三角形与△MCD相似，求所有满足条件的点N的坐标．
（3）在抛物线上是否存在点P，使S△PBD=6？若存在，求出点P的坐标；若不存在，说明理由．
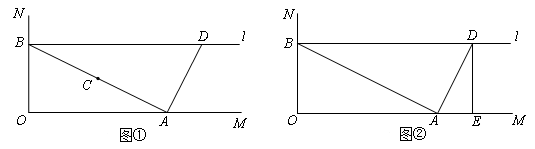
如图，∠MON=90°，A、B分别是OM、ON上的点，OB=4．点C是线段AB的中点，将线段AC以点A为旋转中心，沿顺时针方向旋转90°，得到线段AD，过点B作ON的垂线
．
（1）当点D恰好落在垂线上时，求OA的长；
（2）过点D作DE⊥OM于点E，将（1）问中的△AOB以每秒2个单位的速度沿射线OM方向平移，记平移中的△AOB为△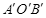
，当点O′与点E重合时停止平移．设平移的时间为t秒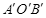，△与△DAE重叠部分的面积为S，请直接写出S与t之间的函数关系式以及自变量t的取值范围；
（3）在（2）问的平移过程中，若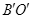
与线段
交于点P，连接
，
，
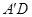，是否存在这样的t，使△
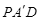是等腰三角形？若存在，求出t的值；若不存在，请说明理由．