如图,∠MON=90°,A、B分别是OM、ON上的点,OB=4.点C是线段AB的中点,将线段AC以点A为旋转中心,沿顺时针方向旋转90°,得到线段AD,过点B作ON的垂线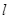 .
.
(1)当点D恰好落在垂线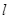 上时,求OA的长;
上时,求OA的长;
(2)过点D作DE⊥OM于点E,将(1)问中的△AOB以每秒2个单位的速度沿射线OM方向平移,记平移中的△AOB为△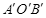 ,当点O′与点E重合时停止平移.设平移的时间为t秒,△
,当点O′与点E重合时停止平移.设平移的时间为t秒,△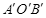 与△DAE重叠部分的面积为S,请直接写出S与t之间的函数关系式以及自变量t的取值范围;
与△DAE重叠部分的面积为S,请直接写出S与t之间的函数关系式以及自变量t的取值范围;
(3)在(2)问的平移过程中,若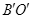 与线段
与线段 交于点P,连接
交于点P,连接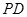 ,
, ,
,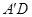 ,是否存在这样的t,使△
,是否存在这样的t,使△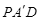 是等腰三角形?若存在,求出t的值;若不存在,请说明理由.
是等腰三角形?若存在,求出t的值;若不存在,请说明理由.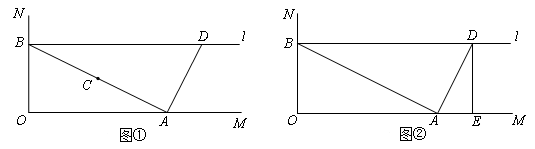
如果三角形有一边上的中线恰好等于这边的长,那么称这个三角形为“匀称三角形”.
(1)已知:如图1,在△ABC中,∠C=90°, .
.
求证:△ABC是“匀称三角形”;
(2)在平面直角坐标系xoy中,如果三角形的一边在x轴上,且这边的中线恰好等于这边的长,我们又称这个三角形为“水平匀称三角形”.如图2,现有10个边长是1的小正方形组成的长方形区域记为G, 每个小正方形的顶点称为格点,A(3,0),B(4,0),若C、D(C、D两点与O不重合)是x轴上的格点,且点C在点A的左侧.在G内使△PAC与△PBD都是“水平匀称三角形”的点P共有几个?其中是否存在横坐标为整数的点P,如果存在请求出这个点P的坐标,如果不存在请说明理由.
在等边三角形ABC中,AD⊥BC于点D.
(1)如图1,请你直接写出线段AD与BC之间的数量关系: AD=BC ;
(2)如图2,若P是线段BC上一个动点(点P不与点B、C重合),联结AP,将线段AP绕点A逆时针旋转60°,得到线段AE,联结CE,猜想线段AD、CE、PC之间的数量关系,并证明你的结论;
(3)如图3,若点P是线段BC延长线上一个动点,(2)中的其他条件不变,按照(2)中的作法,请在图3中补全图形,并直接写出线段AD、CE、PC之间的数量关系.
在平面直角坐标系xOy中,已知二次函数 的图象与x轴的正半轴交于A
的图象与x轴的正半轴交于A 、B
、B 两点(点A在点B的左侧),与y轴交于点C .点A和点B间的距离为2, 若将二次函数
两点(点A在点B的左侧),与y轴交于点C .点A和点B间的距离为2, 若将二次函数 的图象沿y轴向上平移3个单位时,则它恰好过原点,且与x轴两交点间的距离为4.
的图象沿y轴向上平移3个单位时,则它恰好过原点,且与x轴两交点间的距离为4.
(1)求二次函数 的表达式;
的表达式;
(2)在二次函数 的图象的对称轴上是否存在一点P,使点P到B、C两点距离之差最大?若存在,求出点P坐标;若不存在,请说明理由;
的图象的对称轴上是否存在一点P,使点P到B、C两点距离之差最大?若存在,求出点P坐标;若不存在,请说明理由;
(3)设二次函数 的图象的顶点为D,在x轴上是否存在这样的点F,使得
的图象的顶点为D,在x轴上是否存在这样的点F,使得 ?若存在,求出点F的坐标;若不存在,请说明理由.
?若存在,求出点F的坐标;若不存在,请说明理由.
如图,在平面直角坐标系xoy中,E(8,0),F(0 , 6).
(1)当G(4,8)时,则∠FGE=°
(2)在图中的网格区域内找一点P,使∠FPE=90°且四边形OEPF被过P点的一条直线分割成两部分后,可以拼成一个正方形.
要求:写出点P点坐标,画出过P点的分割线并指出分割线(不必说明理由,不写画法).
已知:如图, AB是⊙O的直径,AM和BN是⊙O的两条切线,点D是AM上一点,联结OD , 作BE∥OD交⊙O于点E, 联结DE并延长交BN于点C.
(1)求证:DC是⊙O的切线;
(2)若AD=l,BC=4,求直径AB的长. 