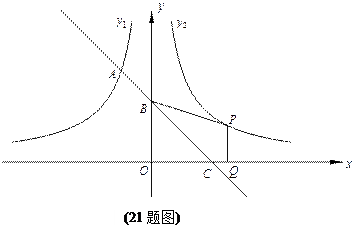
如图,一次函数的图象与反比例函数y1=" –" ( x<0)的图象相交于A点,与y轴、x轴分别相交于B、C两点,且C(2,0).当x<–1时,一次函数值大于反比例函数的值,当x>–1时,一次函数值小于反比例函数值.
(1) 求一次函数的解析式;
(2) 设函数y2= (x>0)的图象与y1=" –" (x<0)的图象关于y轴对称.在y2= (x>0)的图象上取一点P(P点的横坐标大于2),过P作PQ⊥x轴,垂足是Q,若四边形BCQP的面积等于2,求P点的坐标.
 |
解方程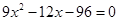
计算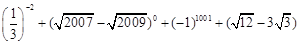
教室里放有一台饮水机(如图),饮水机上有两个放水管,课间时同学们依次到饮水机前用茶杯接水.假设接水过程中水不发生泼洒,每个同学所接的水量都是相等的.两个放水管同时打开时,它们的流量相同,如果放水时先打开一个水管,2分钟时,再打开第二个水管,放水过程中阀门一直开着.饮水机的存水量(升)与放水时间(分钟)的关系如下表所示:

(1)当两个放水管都打开时求每分钟的总出水量;
(2)如果从开始到2分钟时恰好有4个同学接水结束,则前22个同学接水结束共需几分钟?
(3)按(2)的放水方法,求出在课间10分钟内班级中最多有多少个同学能及时接完水?
如图,线段AB= 8cm,C是线段AB上一点,AC=3.2cm,M是AB的中点,N是AC的中点,求线段MN的长
小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示.根据图中数据 (单位:m),解答下列问题:
(1)写出用含x、y的式子表示地面的总面积;
(2)如果y=1.5m,且地面总面积是卫生间面积的15倍,铺1m2地砖的平均费用为80元,求铺地砖的总费用为多少元?