计算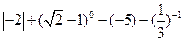：-优题课

某校七年级共有500名学生，在“世界读书日”前夕，开展了“阅读助我成长”的读书活动．为了解该年级学生在此次活动中课外阅读情况，随机抽取 $m$ 名学生，调查他们课外阅读书籍的数量，将收集的数据整理成如下统计表和扇形图．

学生读书数量统计表

阅读量 $/$ 本	学生人数
1	15
2	$a$
3	$b$
4	5

（1）直接写出 $m$ 、 $a$ 、 $b$ 的值；

（2）估计该年级全体学生在这次活动中课外阅读书籍的总量大约是多少本？

解方程组： $\{\begin{matrix} x + y = 10 \\ 2 x + y = 16 \end{matrix}$

如图1，抛物线 $C_{1} : y = a x^{2} - 2 ax + c (a < 0)$ 与 $x$ 轴交于 $A$ 、 $B$ 两点，与 $y$ 轴交于点 $C$ ．已知点 $A$ 的坐标为 $(- 1, 0)$ ，点 $O$ 为坐标原点， $OC = 3 OA$ ，抛物线 $C_{1}$ 的顶点为 $G$ ．

（1）求出抛物线 $C_{1}$ 的解析式，并写出点 $G$ 的坐标；

（2）如图2，将抛物线 $C_{1}$ 向下平移 $k (k > 0)$ 个单位，得到抛物线 $C_{2}$ ，设 $C_{2}$ 与 $x$ 轴的交点为 $A'$ 、 $B'$ ，顶点为 $G'$ ，当△ $A' B' G'$ 是等边三角形时，求 $k$ 的值：

（3）在（2）的条件下，如图3，设点 $M$ 为 $x$ 轴正半轴上一动点，过点 $M$ 作 $x$ 轴的垂线分别交抛物线 $C_{1}$ 、 $C_{2}$ 于 $P$ 、 $Q$ 两点，试探究在直线 $y = - 1$ 上是否存在点 $N$ ，使得以 $P$ 、 $Q$ 、 $N$ 为顶点的三角形与 $ΔAOQ$ 全等，若存在，直接写出点 $M$ ， $N$ 的坐标：若不存在，请说明理由．

我们知道，有理数包括整数、有限小数和无限循环小数，事实上，所有的有理数都可以化为分数形式（整数可看作分母为1的分数），那么无限循环小数如何表示为分数形式呢？请看以下示例：

例：将 $0 . \dot{7}$ 化为分数形式

由于 $0 . \dot{7} = 0.777 \dots$ ，设 $x = 0.777 \dots$ ①

则 $10 x = 7.777 \dots$ ②

② $-$ ①得 $9 x = 7$ ，解得 $x = \frac{7}{9}$ ，于是得 $0 . \dot{7} = \frac{7}{9}$ ．

同理可得 $0 . \dot{3} = \frac{3}{9} = \frac{1}{3}$ ， $1 . \dot{4} = 1 + 0 . \dot{4} = 1 + \frac{4}{9} = \frac{13}{9}$

根据以上阅读，回答下列问题：（以下计算结果均用最简分数表示）

（基础训练）

（1） $0 . \dot{5} =$ 　　， $5 . \dot{8} =$ 　　；

（2）将 $0 . \dot{2} \dot{3}$ 化为分数形式，写出推导过程；

（能力提升）

（3） $0 . \dot{3} 1 \dot{5} =$ 　　， $2.0 \dot{1} \dot{8} =$ 　　；

（注 $: 0 . \dot{3} 1 \dot{5} = 0.315315 \dots$ ， $2.0 \dot{1} \dot{8} = 2.01818 \dots)$

（探索发现）

（4）①试比较 $0 . \dot{9}$ 与1的大小： $0 . \dot{9}$ 　　1（填“ $>$ ”、“ $<$ ”或“ $=$ ” $)$

②若已知 $0 . \dot{2} 8571 \dot{4} = \frac{2}{7}$ ，则 $3 . \dot{7} 1428 \dot{5} =$ 　　．

（注 $: 0 . \dot{2} 8571 \dot{4} = 0.285714285714 \dots)$

为迎接“世界华人炎帝故里寻根节”，某工厂接到一批纪念品生产订单，按要求在15天内完成，约定这批纪念品的出厂价为每件20元，设第 $x$ 天（ $1 ⩽ x ⩽ 15$ ，且 $x$ 为整数）每件产品的成本是 $p$ 元， $p$ 与 $x$ 之间符合一次函数关系，部分数据如表：

天数 $(x)$	1	3	6	10
每件成本 $p$ （元）	7.5	8.5	10	12

任务完成后，统计发现工人李师傅第 $x$ 天生产的产品件数 $y$ （件）与 $x$ （天）满足如下关系： $y = \{\begin{matrix} 2 x + 20 (1 ⩽ x < 10, 且 x 为整数) \\ 40 (10 ⩽ x ⩽ 15, 且 x 为整数) \end{matrix}$

设李师傅第 $x$ 天创造的产品利润为 $W$ 元．

（1）直接写出 $p$ 与 $x$ ， $W$ 与 $x$ 之间的函数关系式，并注明自变量 $x$ 的取值范围：

（2）求李师傅第几天创造的利润最大？最大利润是多少元？

（3）任务完成后，统计发现平均每个工人每天创造的利润为299元．工厂制定如下奖励制度：如果一个工人某天创造的利润超过该平均值，则该工人当天可获得20元奖金．请计算李师傅共可获得多少元奖金？