在直角坐标系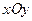 中,直线
中,直线 的参数方程为
的参数方程为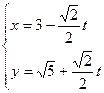 (
(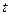 为参数),在极
为参数),在极
坐标系(与直角坐标系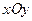 取相同的长度单位,且以原点O为极点,以
取相同的长度单位,且以原点O为极点,以 轴正半轴为极轴)中,圆C的方程为
轴正半轴为极轴)中,圆C的方程为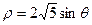 。
。
①求圆C的直角坐标方程;
②设圆C与直线 交于点A、B,若点P的坐标为
交于点A、B,若点P的坐标为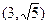 ,求|PA|+|PB|。
,求|PA|+|PB|。
已知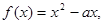

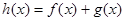 .
.
(1)若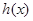 的单调减区间是
的单调减区间是 ,求实数
,求实数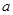 的值;
的值;
(2)若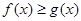 对于定义域内的任意
对于定义域内的任意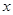 恒成立,求实数
恒成立,求实数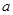 的取值范围;
的取值范围;
(3)设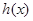 有两个极值点
有两个极值点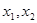 , 且
, 且 若
若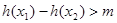 恒成立,求
恒成立,求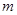 的最大值.
的最大值.
已知函数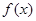 定义在
定义在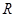 上,对任意的
上,对任意的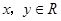 ,
,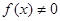 ,且
,且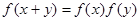 .
.
(1)求 ,并证明:
,并证明: ;
;
(2)若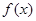 单调,且
单调,且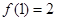 .设向量
.设向量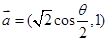 ,
, ,对任意
,对任意 ,
, 恒成立,求实数
恒成立,求实数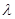 的取值范围.
的取值范围.
已知函数 在
在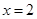 处有极大值.
处有极大值.
(1)当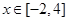 时,函数
时,函数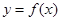 的图象在抛物线
的图象在抛物线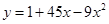 的下方,求
的下方,求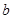 的取值范围.
的取值范围.
(2)若过原点有三条直线与曲线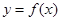 相切,求
相切,求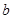 的取值范围;
的取值范围;
等差数列 的首项为23,公差为整数,且第6项为正数,从第7项起为负数。
的首项为23,公差为整数,且第6项为正数,从第7项起为负数。
(1)求此数列的公差d;
(2)当前n项和 是正数时,求n的最大值。
是正数时,求n的最大值。
已知向量 ,设函数
,设函数
(1)求 在区间
在区间 上的零点;
上的零点;
(2)在 中,角
中,角 的对边分别是
的对边分别是 ,且满足
,且满足 ,求
,求 的取值范围.
的取值范围.