已知一家公司生产某种品牌服装的年固定成本为10万元,每生产1千件需另投入2.7万元。设该公司一年内生产该品牌服装x千件并全部销售完,每千件的销售收入为
R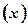 万元,且R
万元,且R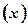
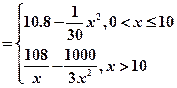 (1)写出年利润
(1)写出年利润 关于年产量
关于年产量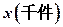 的函数解析式;
的函数解析式;
(2)年产量为多少千件时,该公司在这一品牌服装的生产中所获得的年利润最大。
(注:年利润=年销售收入-年总成本)
某教授为了测试贫困地区和发达地区的同龄儿童的智力,出了10个智力题,每个题10分,然后作了统计,结果如下:
贫困地区
| 参加测试的人数 |
30 |
50 |
100 |
200 |
500 |
800 |
| 得60分以上的人数 |
16 |
27 |
52 |
104 |
256 |
402 |
| 得60分以上的频率 |
发达地区
| 参加测试的人数 |
30 |
50 |
100 |
200 |
500 |
800 |
| 得60分以上的人数 |
17 |
29 |
56 |
111 |
276 |
440 |
| 得60分以上的频率 |
(1)计算两地区参加测试的儿童得60分以上的频率;
(2)求两个地区参加测试的儿童得60分以上的概率;
(3)分析贫富差距为什么会带来人的智力的差别.
以下是在某地的旧房屋的销售价格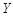 和房屋的面积x的数据:
和房屋的面积x的数据:
房屋面积(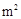 ) ) |
115 |
110 |
80 |
135 |
105 |
| 销售价格(万元) |
24.8 |
21.6 |
18.4 |
29.2 |
22 |
(1)画出数据对应的散点图;
(2)求线性回归方程,并在散点图中画出回归直线;
(3)据(2)的结果估计当房屋面积为150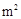 时的销售价格.
时的销售价格.
一个机器由于使用时间较长,生产的零件有一些会有缺损,按不同转速生产出来的零件有缺损的统计数据如下:
如果y与x线性相关,求回归直线方程.
一个工厂在某年里每月产品的总成本y(万元)与该月产量x(万件)之间有如下一组对应数据:
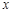 |
1.08 |
1.12 |
1.19 |
1.28 |
1.36 |
1.48 |
1.59 |
1.68 |
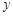 |
2.25 |
2.37 |
2.40 |
2.55 |
2.64 |
2.75 |
2.92 |
3.03 |
判断它们是否有相关关系.
(本题满分14分)设有关于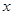 的一元二次方程
的一元二次方程 .
.
(1)若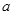 是从0,1,2,3四个数中任取的一个数,
是从0,1,2,3四个数中任取的一个数, 是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
(2)若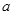 是从区间[0,3]任取的一个数,
是从区间[0,3]任取的一个数, 是从区间[0,2]任取的一个数,求上述方程有实根的概率.
是从区间[0,2]任取的一个数,求上述方程有实根的概率.