已知一家公司生产某种品牌服装的年固定成本为10万元,每生产1千件需另投入2.7万元。设该公司一年内生产该品牌服装x千件并全部销售完,每千件的销售收入为R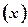 万元,且R
万元,且R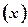
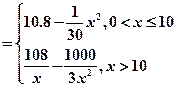
(1)写出年利润 关于年产量
关于年产量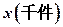 的函数解析式;
的函数解析式;
(2)年产量为多少千件时,该公司在这一品牌服装的生产中所获得的年利润最大。
(注:年利润=年销售收入-年总成本)
设函数 ,
, .
.
(1)记 为
为 的导函数,若不等式
的导函数,若不等式 在
在 上有解,求实数
上有解,求实数 的取值范围;
的取值范围;
(2)若 ,对任意的
,对任意的 ,不等式
,不等式 恒成立.求
恒成立.求 (
( ,
, )的值.
)的值.
已知在直角坐标系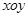 中,曲线
中,曲线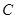 的参数方程为
的参数方程为 (
(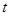 为非零常数,
为非零常数,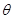 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系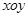 取相同的长度单位,且以原点
取相同的长度单位,且以原点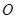 为极点,以
为极点,以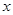 轴正半轴为极轴)中,直线
轴正半轴为极轴)中,直线 的方程为
的方程为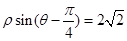 .
.
(Ⅰ)求曲线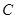 的普通方程并说明曲线的形状;
的普通方程并说明曲线的形状;
(Ⅱ)是否存在实数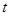 ,使得直线
,使得直线 与曲线
与曲线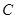 有两个不同的公共点
有两个不同的公共点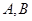 ,且
,且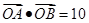 (其中
(其中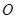 为坐标原点)?若存在,请求出;否则,请说明理由.
为坐标原点)?若存在,请求出;否则,请说明理由.
某市统计局就本地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示月收入在 ,(单位:元).
,(单位:元).
(Ⅰ)估计居民月收入在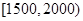 的概率;
的概率;
(Ⅱ)根据频率分布直方图估计样本数据的中位数;
(Ⅲ)若将频率视为概率,从本地随机抽取3位居民(看做有放回的抽样),求月收入在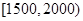 的居民数X的分布列和数学期望.
的居民数X的分布列和数学期望.
已知函数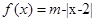 ,
,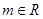 ,且
,且 的解集为
的解集为 .
.
(1)求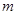 的值;
的值;
(2)若 ,且
,且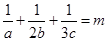 ,求
,求 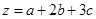 的最小值.
的最小值.
已知函数f(x)= x
x -ax+(a-1)
-ax+(a-1)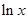 ,
,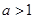 .
.
(1)讨论函数 的单调性;(2)若
的单调性;(2)若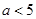 ,设
,设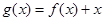 ,
,
(ⅰ)求证g(x)为单调递增函数;
(ⅱ)求证对任意x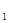 ,x
,x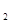
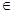
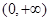 ,x
,x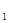
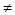 x
x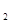 ,有
,有 .
.