(本小题满分14分)已知f (x)=mx(m为常数,m>0且m≠1).设f (a1),f (a2),…,f (an),…(n∈N)是首项为m2,公比为m的等比数列.
(1)求证:数列{an}是等差数列;
(2)若bn=an f (an),且数列{bn}的前n项和为Sn,当m=3时,求Sn;
(3)若cn= f(an) lg f (an),问是否存在m,使得数列{cn}中每一项恒不小于它后面的项?若存在,求出m的取值范围;若不存在,请说明理由.
已知数列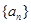 为等差数列,其中
为等差数列,其中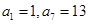 .
.
(1)求数列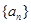 的通项公式;
的通项公式;
(2)若数列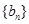 满足
满足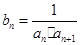 ,
, 为数列
为数列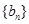 的前
的前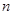 项和,当不等式
项和,当不等式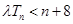 (
(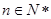 )恒成立时,求实数
)恒成立时,求实数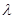 的取值范围.
的取值范围.
为了降低能源损耗,某体育馆的外墙需要建造隔热层.体育馆要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度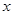 (单位:cm)满足关系:
(单位:cm)满足关系: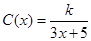 (
(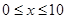 ,
,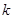 为常数),若不建隔热层,每年能源消耗费用为8万元.设
为常数),若不建隔热层,每年能源消耗费用为8万元.设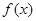 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.
(1)求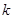 的值及
的值及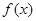 的表达式;
的表达式;
(2)隔热层修建多厚时,总费用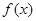 达到最小?并求最小值.
达到最小?并求最小值.
在 中,角
中,角 所对的边分别为
所对的边分别为 ,已知
,已知 ,
,
(1)求 的大小;
的大小;
(2)若 ,求
,求 的取值范围.
的取值范围.
在 中,角
中,角 所对的边分别是
所对的边分别是 ,若
,若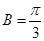 ,且
,且 .
.
(1)求 的值;
的值;
(2)若 ,求
,求 的面积.
的面积.
某校高三年级学生600名,从参加期中考试的学生中随机抽出某班学生(该班共50名同学),并统计了他们的数学成绩(成绩均为整数且满分为150分),数学成绩分组及各组频数如下表:
| 分组 |
频数 |
频率 |
 |
2 |
0.04 |
 |
4 |
0.08 |
 |
8 |
0.16 |
 |
11 |
0.22 |
 |
15 |
0.30 |
 |
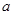 |
 |
 |
4 |
0.08 |
| 合计 |
50 |
1 |
(1)写出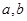 的值;
的值;
(2)估计该校高三学生数学成绩在120分以上学生人数;
(3)该班为提高整体数学成绩,决定成立“二帮一”小组,即从成绩在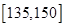 中选两位同学,来帮助成绩在
中选两位同学,来帮助成绩在 中的某一位同学,已知甲同学的成绩为56分,乙同学的成绩为145分,求甲乙在同一小组的概率.
中的某一位同学,已知甲同学的成绩为56分,乙同学的成绩为145分,求甲乙在同一小组的概率.