已知圆:x2+y2-4x-6y+12=0,(1)求过点 的圆的切线方程;
的圆的切线方程;
(2)点 为圆上任意一点,求
为圆上任意一点,求 的最值。
的最值。
已知数列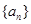 是一个等差数列,
是一个等差数列, 是其前
是其前 项和,且
项和,且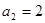 ,
,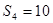 .
.
(1)求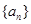 的通项
的通项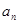 ;
;
(2)求数列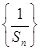 的前10项的和
的前10项的和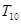
为了研究某种细菌随时间x变化的繁殖个数,收集数据如下:
天数 |
1 |
2 |
3 |
4 |
5 |
6 |
繁殖个数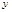 |
6 |
12 |
25 |
49 |
95 |
190 |
(1)作出这些数据的散点图;
(2)求出y对x的回归方程.
设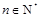 ,圆
,圆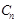 :
: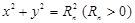 与
与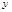 轴正半轴的交点为
轴正半轴的交点为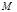 ,与曲线
,与曲线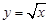 的交点为
的交点为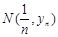 ,直线
,直线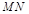 与
与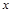 轴的交点为
轴的交点为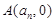 .
.
(1)用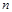 表示
表示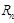 和
和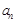 ;
;
(2)求证: ;
;
(3)设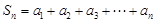 ,
,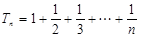 ,求证:
,求证: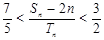 .
.
当实数m为何值时,z=lg(m2-2m-2)+(m2+3m+2)i
(1)为纯虚数;
(2)为实数;
(3)对应的点在复平面内的第二象限内.
已知关于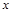 的方程
的方程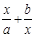 =1,其中
=1,其中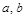 为实数.
为实数.
(1)若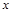 =1-
=1-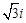 是该方程的根,求
是该方程的根,求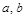 的值.
的值.
(2)当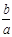 >
>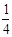 且
且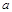 >0时,证明该方程没有实数根.
>0时,证明该方程没有实数根.