要将两种厚度、材质相同,大小不同的钢板截成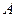 、
、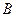 、
、 三种规格的成品.每
三种规格的成品.每
张钢板可同时截得三种规格的块数如下表: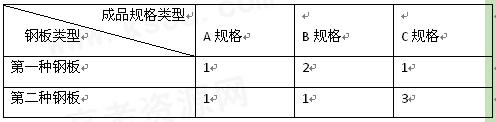
每张钢板的面积:第一张为 ,第二张为
,第二张为 .今需要
.今需要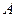 、
、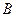 、
、 三种规格的成品各为12、15、27块.则两种钢板各截多少张,可得所需三种规格的成品,且使所用钢板的面积最少?
三种规格的成品各为12、15、27块.则两种钢板各截多少张,可得所需三种规格的成品,且使所用钢板的面积最少?
某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数,得到如下资料:
| 日期 |
12月1日 |
12月2日 |
12月3日 |
12月4日 |
12月5日 |
温差 (°C) (°C) |
10 |
11 |
13 |
12 |
8 |
发芽数 (颗) (颗) |
23 |
25 |
30 |
26 |
16 |
该农科所确定的研究方案是:先从这五组数据中选取2组,用剩下的3组数据求线性回归方程,再对被选取的2组数据进行检验.
(1)求选取的2组数据恰好是不相邻2天数据的概率;
(2)若选取的是12月1日与12月5日的两组数据,请根据12月2日至12月4日的数据,求出y关于x的线性回归方程 已知回归直线方程是:
已知回归直线方程是: ,其中
,其中 ,
, ;
;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?
在人群流量较大的街道,有一中年人吆喝“送钱”,只见他手拿一黑色小布袋,袋中有3只黄色、3只白色的乒乓球(其体积、质地完成相同),旁边立着一块小黑板写道:
摸球方法:从袋中随机摸出3个球,若摸得同一颜色的3个球,摊主送给摸球者5元钱;若摸得非同一颜色的3个球,摸球者付给摊主1元钱。
(1)摸出的3个球为白球的概率是多少?
(2)摸出的3个球为2个黄球1个白球的概率是多少?
(3)假定一天中有100人次摸奖,试从概率的角度估算一下这个摊主一个月(按30天计)能赚多少钱?
向面积为 的
的 内任投一点
内任投一点 ,求
,求 的面积小于
的面积小于 的概率?
的概率?
某市一公交线路某区间内共设置六个公交站点(如图所示),分别为 ,现在甲、乙两人同时从
,现在甲、乙两人同时从 站上车,且他们中的每个人在站点
站上车,且他们中的每个人在站点 下车是等可能。
下车是等可能。
求(1)甲在 或
或 站点下车的概率
站点下车的概率
(2)甲、乙两人不在同一站点下车的概率
为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛. 为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计. 请你根据尚未完成并有局部污损的频率分布表和频数分布直方图,解答下列问题:
(1)填充频率分布表的空格(将答案直接填在表格内);
| 分组 |
频数 |
频率 |
| 50.5~60.5 |
4 |
0.08 |
| 60.5~70.5 |
0.16 |
|
| 70.5~80.5 |
10 |
|
| 80.5~90.5 |
16 |
0.32 |
| 90.5~100.5 |
||
| 合计 |
50 |
(2)补全频数条形图;
(3)若成绩在75.5~85.5分的学生为二等奖,问获得二等奖的学生约为多少人。